数据分析基础 (上)

Data Analytics Introduction - Part 1

范叶亮 Leo Van

目录

• NumPy 简介
• 多维数组对象
• 面向数组编程

NumPy 简介

NumPy 简介

NumPy 是使用 Python 进行科学计算的基础软件包。它包括：

• 功能强大的 N 维数组对象。
• 精密广播功能函数。
• 集成 C/C++ 和 Fortran 代码的工具。
• 强大的线性代数、傅立叶变换和随机数功能。

NumPy 包的核心是 ndarray 对象。它封装了 Python 原生的同数据类型的 N 维数组，为了保证其性能优良，其中有许多操作都是代码在本地进行编译后执行的。

在后续内容中，我们会使用下面的快捷方式导入 NumPy：

import numpy as np

NumPy 简介

NumPy 数组和原生 Python Array（数组）之间有几个重要的区别：

• NumPy 数组在创建时具有固定的大小，与 Python 的原生数组对象（可以动态增长）不同。更改 ndarray 的大小将创建一个新数组并删除原来的数组。
• NumPy 数组中的元素都需要具有相同的数据类型，因此在内存中的大小相同。 例外情况：Python 的原生数组里包含了 NumPy 的对象的时候，这种情况下就允许不同大小元素的数组。
• NumPy 数组有助于对大量数据进行高级数学和其他类型的操作。通常，这些操作的执行效率更高，比使用 Python 原生数组的代码更少。
• 越来越多的基于 Python 的科学和数学软件包使用 NumPy 数组，虽然这些工具通常都支持 Python 的原生数组作为参数，但它们在处理之前会还是会将输入的数组转换为 NumPy 的数组，而且也通常输出为 NumPy 数组。

NumPy 简介

NumPy 的高效得益于向量化和广播：

向量化描述了代码中没有任何显式的循环，索引等。这些当然是预编译的 C 代码中“幕后”优化的结果。向量化代码有许多优点，其中包括：

• 向量化代码更简洁，更易于阅读
• 更少的代码行通常意味着更少的错误
• 代码更接近于标准的数学符号（通常，更容易正确编码数学结构）
• 向量化导致产生更多 “Pythonic” 代码。如果没有向量化，我们的代码就会被低效且难以阅读的 for 循环所困扰。

广播是用于描述操作的隐式逐元素行为的术语。 一般来说，在 NumPy 中，所有操作，不仅仅是算术运算，逻辑，位，功能等，都以这种隐式的逐元素方式进行广播。有关广播的详细“规则”，请参阅 numpy.doc.broadcasting。

多维数组对象

数据类型

NumPy 支持比 Python 更多种类的数据类型，NumPy 的数值类型实际上是 dtype 对象的实例，并对应唯一的字符。

NumPy 类型	类型代码	描述
int8, uint8	i1, u1	有符号和无符号的 8 位整数
int16, uint16	i2, u2	有符号和无符号的 16 位整数
int32, uint32	i4, u4	有符号和无符号的 32 位整数
int64, uint64	i8, u8	有符号和无符号的 64 位整数
float16	f2	半精度浮点数
float32	f4 或 f	标准单精度浮点数，兼容 C 语言 float
float64	f8 或 d	标准双精度浮点数，兼容 C 语言 double 和 Python float

数据类型

NumPy 类型	类型代码	描述
float128	f16 或 g	拓展精度浮点数
complex64, complex128, complex256
bool	?	布尔值，True 或 False
object	O	Python object 类型
string_	S	修正的 ASCII 字符串类型，长度为 10 的字符串类型，使用 S10。
unicode_	U	修正的 Unicode 类型，长度为 10 的 Unicode 类型，使用 U10。

创建数组

生成数组最简单的方式就是使用 array 函数。array 函数接收任意的序列类型对象（也包括其他的数组），生成一个新的包含传递数据的 NumPy 数组。

a1 = np.array([1, 2.0, 3])
a1

array([1., 2., 3.])

嵌套序列会自动转换成多维数组：

a2 = np.array([[1, 2, 3], [4, 5, 6]])
a2

array([[1, 2, 3],
       [4, 5, 6]])

可以通过 ndim 和 shape 属性确定数组的维度和形状：

a2.ndim

2

a2.shape

(2, 3)

除非显式的指定，否则 np.array 会自动推断数组的数据类型。数据类型存储在一个特殊的元数据 dtype 中：

a1.dtype

dtype('float64')

a1.dtype

dtype('float64')

创建数组

NumPy 还可以通过其他函数生成数组，如下表所示：

函数名	描述
array	将输入数据转换为 ndarray，如不显式指明数据类型，则自动推断，复制所有输入数据
asarray	将输入转换为 ndarray，但如果输入已经是 ndarray 则不在复制
arange	Python 内建函数 range 的数组版，返回一个数组
ones, ones_like	根据给定形状和数据类型生成全 1 数组，根据给定数组生成形状一样的全 1 数组
zeros, zeros_like	根据给定形状和数据类型生成全 0 数组，根据给定数组生成形状一样的全 0 数组
empty, empty_like	根据给定形状和数据类型生成空数组，根据给定数组生成形状一样的空数组
full, full_like	根据给定形状和数据类型生成指定数值的数组，根据给定数组生成形状一样的指定数值的数组
eye, indentity	生成一个 \(N \times N\) 的特征矩阵（对角线值为 1，其余为 0）

数组算术

NumPy 允许批量运算而无需任何 for 循环，该特性称之为向量化，任何两个等尺寸数组之间的算数操作搜是逐元素的：

arr = np.array([[1., 2., 3.], [4., 5., 6.]])
arr * arr

array([[ 1.,  4.,  9.],
       [16., 25., 36.]])

arr - arr

array([[0., 0., 0.],
       [0., 0., 0.]])

标量计算的算术操作会把参数传递给数组的每个元素：

1 / arr

array([[1.        , 0.5       , 0.33333333],
       [0.25      , 0.2       , 0.16666667]])

arr ** 0.5

array([[1.        , 1.41421356, 1.73205081],
       [2.        , 2.23606798, 2.44948974]])

同尺寸数组之间的比较会产生一个布尔值数组 。

广播

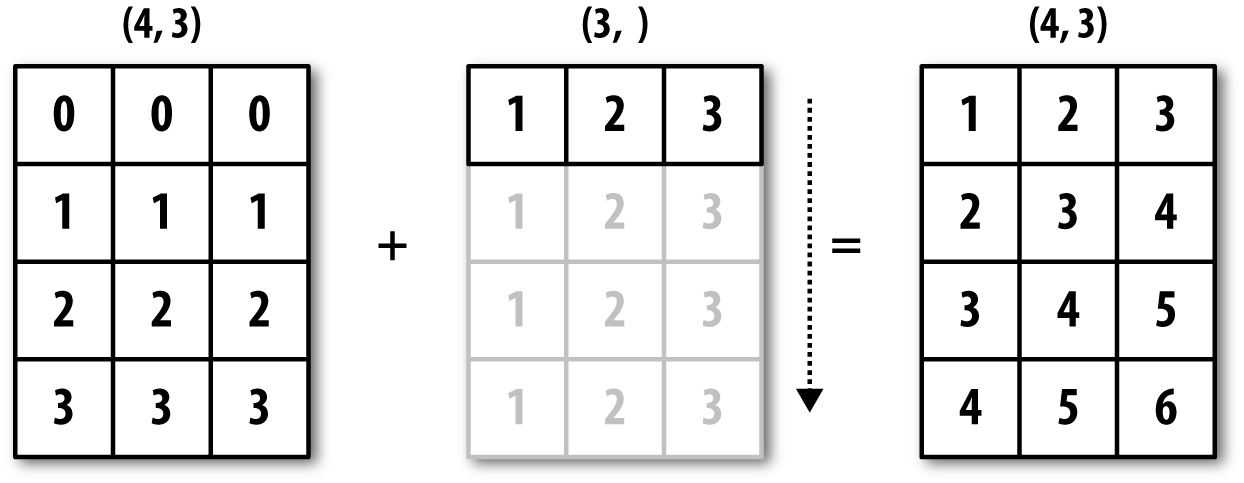
广播描述了算法如何在不同形状的数组之间进行运算，它功能强大，但也可能会导致混淆。广播的原则：如果对于每个结尾维度（即从尾部开始的），轴长度都匹配或者长度都是 1， 两个数组就是可以兼容广播的。之后，广播会在丢失的或长度为 1 的轴上进行。

arr = np.random.randn(4, 3)
arr.mean(0)

array([-0.98010244, -0.01454389,  0.95881737])

arr - arr.mean(0)

array([[ 0.68035327, -0.78576366, -0.30692341],
       [-0.48962846,  1.17021947, -0.13110311],
       [-0.11774639,  0.27551998,  0.390758  ],
       [-0.07297843, -0.6599758 ,  0.04726852]])

广播

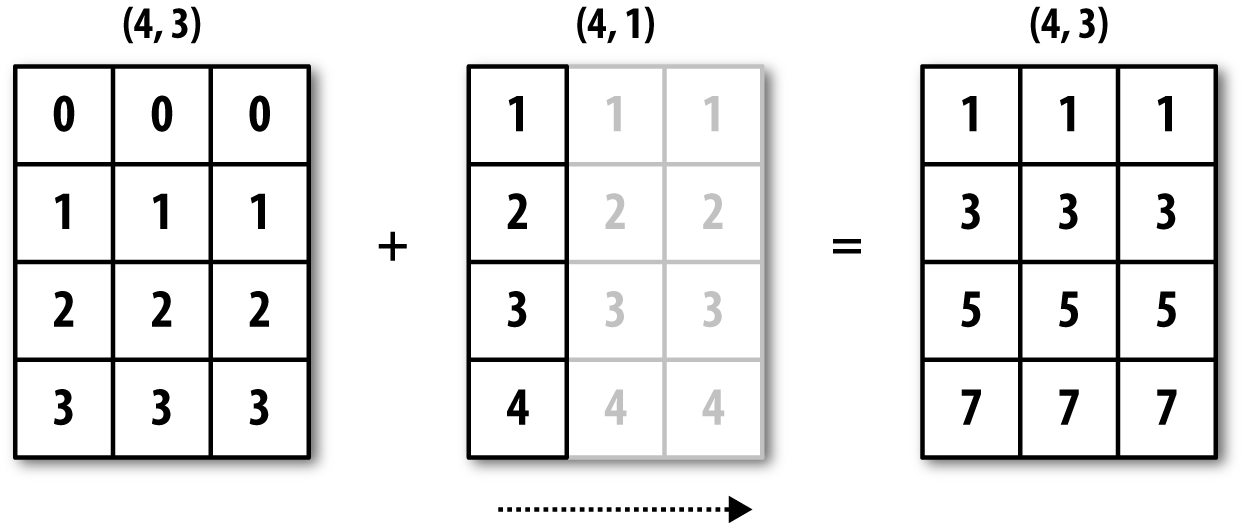
假如我们希望减去每一行的平均值，由于 arr.mean(0) 的长度为 3，因此他与轴 0 上的广播兼容，因为 arr 中的结尾维度为 3，因此匹配。为了从轴 1 减去均值（即从每行减去行平均值），较小的数组的形状必须是 (4, 1)。

arr = np.random.randn(4, 3)
arr - arr.mean(1).reshape((4, 1))

array([[-0.80363195,  1.25793151, -0.45429955],
       [ 0.09531669, -0.35580953,  0.26049285],
       [-1.89341981,  0.39814628,  1.49527353],
       [-0.98384515,  1.78821865, -0.8043735 ]])

广播

下图为对沿着轴将一个二维数组加到三维数组的示意：

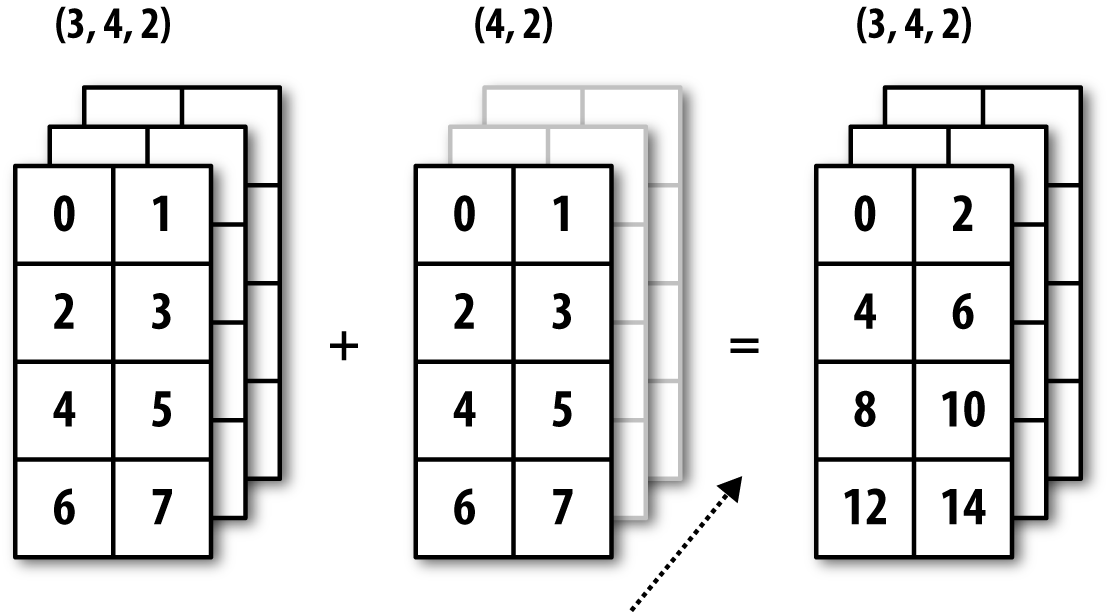
广播

根据广播规则，“广播维度”在较小的数组中须为 1，在“行减均值”的例子中，意味着形状需要是 (4, 1) 而不是 (4, )。使用 reshape 是一种选择，但插入一个轴需要构造一个表示新形状的元组。在三维情况下，任何一个维度上进行广播只是将数据塑造为形状兼容的问题，下图显示了三维数组的每个轴上广播所需的形状：

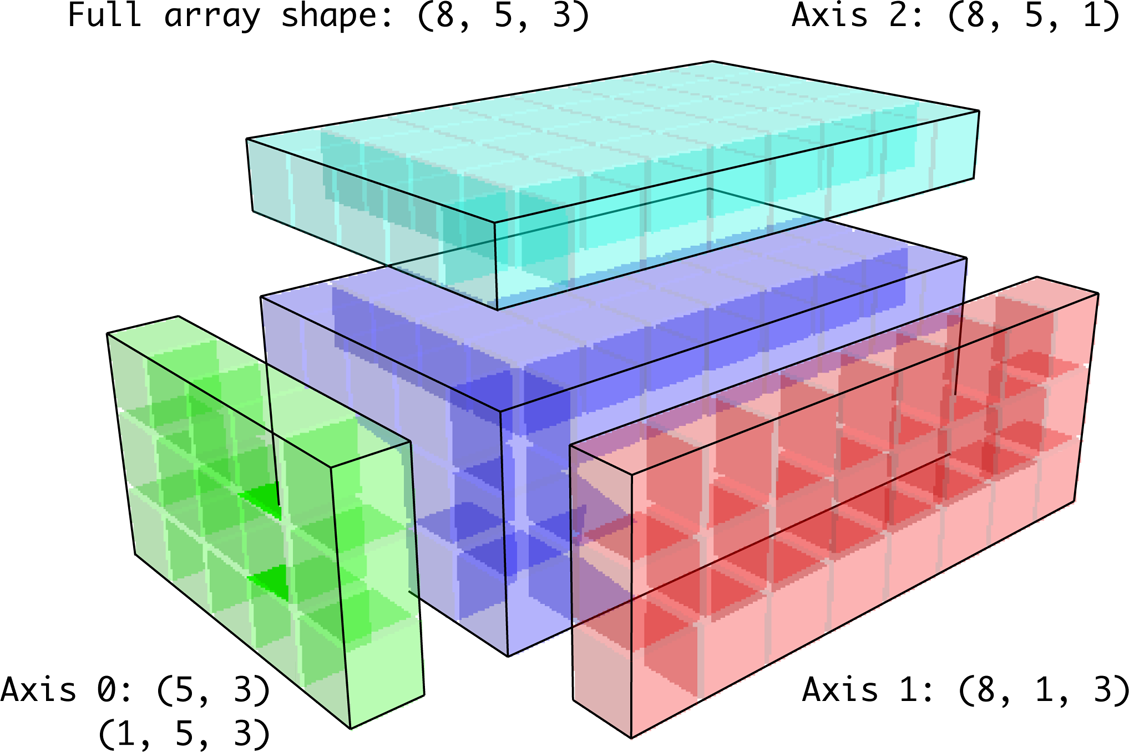
索引

NumPy 的 ndarray 数据可以通过索引和切片进行访问和修改，与 Python 的内建列表类似。

arr = np.arange(6)
arr

array([0, 1, 2, 3, 4, 5])

arr[3]

3

arr[4:6]

array([4, 5])

arr[0:2] = 9
arr

array([9, 9, 2, 3, 4, 5])

当传入一个数值给数组的切片后，数值被传递给了整个切片，这区别于 Python 的内建列表，数组的切片是原数据的视图，这意味着数据并不是被复制了，任何对于视图的修改都会反映到原数组上。

arr_slice = arr[0:2]
arr_slice[:] = 0
arr

array([0, 0, 2, 3, 4, 5])

索引

对于一个二维数组，每个索引值对应的元素不再是一个值，而是一个一维数组。

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
arr[2]

array([7, 8, 9])

通过递归方式或传递索引的逗号分割列表获取元素：

arr[0][2]

3

arr[0, 2]

3

在二维数组上索引，我们可以将 0 轴看做“行”，将 1 轴看做“列”。

索引

在多维数组中，可以省略后续索引值，返回的对象是降低一个维度的数组。

arr = np.array(
    [[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
arr

array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]]])

arr[0]

array([[1, 2, 3],
       [4, 5, 6]])

类似地，arr[1, 0] 返回的是一个一维数组：

arr[1, 0]

array([7, 8, 9])

需要注意的是，以上数组的子集中返回的都是视图。

切片

与 Python 列表的一维对象类似，数组可以通过类似的语法进行切片：

arr = np.array([1, 2, 3, 4, 5, 6])
arr

array([1, 2, 3, 4, 5, 6])

arr[1:3]

array([2, 3])

对于二维数组进行切片略有不同：

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
arr[:2]

array([[1, 2, 3],
       [4, 5, 6]])

数组沿着轴 0 进行切片，表达式 arr[:2] 表示选择 arr 的前两“行”。也可以进行多阻切片：

arr[:2, 1:]

array([[2, 3],
       [5, 6]])

切片

需要注意的是，单独的一个冒号表示选择整个轴上的数组，因此可以按照如下方式在更高维度上进行切片：

arr[:, :1]

array([[1],
       [4],
       [7]])

对整个切片表达式赋值，整个切片都会重新赋值：

arr[:2, 1:] = 0
arr

array([[1, 0, 0],
       [4, 0, 0],
       [7, 8, 9]])

布尔索引

考虑如下例子，每个人名和 data 数组中的一行对应：

names = np.array(
    ['Bob', 'Joe', 'Leo', 'Tom', 'Leo'])
data = np.random.randn(5, 3)
names

array(['Bob', 'Joe', 'Leo', 'Tom', 'Leo'], dtype='<U3')

data

array([[ 0.84803204,  0.59935065, -0.0871786 ],
       [-0.73257303,  1.96105621,  1.53448795],
       [ 0.27710006, -0.59172106,  1.5265431 ],
       [-2.29488734, -0.87514816,  0.21040408],
       [ 1.60378927,  0.75809744, -0.47541769]])

我们想要选中所有 Leo 对应的行，数组的比较操作也是可以向量化的：

names == 'Leo'

array([False, False,  True, False,  True])

在索引数据时可以传入布尔值数组：

data[names == 'Leo']

array([[ 0.27710006, -0.59172106,  1.5265431 ],
       [ 1.60378927,  0.75809744, -0.47541769]])

布尔数组的长度必须和数组轴索引长度一致，不一致时并不会报错，因此建议使用该特性时要注意。

布尔索引

data[names != 'Leo']

array([[ 0.84803204,  0.59935065, -0.0871786 ],
       [-0.73257303,  1.96105621,  1.53448795],
       [-2.29488734, -0.87514816,  0.21040408]])

data[~(names == 'Leo')]

array([[ 0.84803204,  0.59935065, -0.0871786 ],
       [-0.73257303,  1.96105621,  1.53448795],
       [-2.29488734, -0.87514816,  0.21040408]])

data[(names == 'Leo') | (names == 'Bob')]

array([[ 0.84803204,  0.59935065, -0.0871786 ],
       [ 0.27710006, -0.59172106,  1.5265431 ],
       [ 1.60378927,  0.75809744, -0.47541769]])

data[names == 'Leo', 1:]

array([[-0.59172106,  1.5265431 ],
       [ 0.75809744, -0.47541769]])

数组转置和换轴

转置是一种特殊的数据重组形式，可以返回数据的视图而不需要复制任何内容。数组拥有 transpose 方法，也有特殊的 T 属性：

arr = np.arange(12).reshape((3, 4))
arr.T

array([[ 0,  4,  8],
       [ 1,  5,  9],
       [ 2,  6, 10],
       [ 3,  7, 11]])

对于更高维度的数组，transpose 方法可以接受包含轴编号的元素，用于置换轴：

arr = np.arange(16).reshape((2, 2, 4))

arr

array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],

       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]]])

arr.transpose((1, 0, 2))

array([[[ 0,  1,  2,  3],
        [ 8,  9, 10, 11]],

       [[ 4,  5,  6,  7],
        [12, 13, 14, 15]]])

数组转置和换轴

使用 .T 进行转置是换轴的一个特殊案例。ndarray 有一个 swapaxes 方法，该方法接收一堆轴编号作为参数，并对轴进行调整用于重组数据：

arr

array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],

       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]]])

arr.swapaxes(1, 2)

array([[[ 0,  4],
        [ 1,  5],
        [ 2,  6],
        [ 3,  7]],

       [[ 8, 12],
        [ 9, 13],
        [10, 14],
        [11, 15]]])

通用函数

通用函数，也可以称为 ufunc，是一种在 ndarray 数据中进行逐元素操作的函数。某些简单函数接收一个或多个标量数值，并产生一个或多个标量结果，而通用函数就是对这些简单函数的向量化封装。

arr = np.arange(10)
arr

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

np.sqrt(arr)

array([0.        , 1.        , 1.41421356, 1.73205081, 2.        ,
       2.23606798, 2.44948974, 2.64575131, 2.82842712, 3.        ])

这些是所谓的一元通用函数，还有一些通用函数，例如 add 或 maximum 则会接受两个数组并返回一个数组作为结果，因此称之为二元通用函数。

一元通用函数

函数名	描述
abs, fabs	逐元素地计算整数、浮点数或复数的绝对值
sqrt	计算每个元素的平方根（与 arr ** 0.5 相等）
square	计算每个元素的平方（与 arr ** 2 相等）
exp	计算每个元素的自然指数值 \(e^x\)
log, log10, log2, log1p	自然对数（ \(e\) 为底），对数 10 为底，对数 2 为底， \(log \left(1+x\right)\)
sign	计算每个元素的符号值：1 为正数，0 为 0，-1 为负数
ceil	计算每个元素的最高整数值，即向上取整
floor	计算每个元素的最小整数值，即向下取整

一元通用函数

函数名	描述
rint	将元素保留至整数位，并保持 dtype
modf	分别将数组的小数部分和整数部分按数组形式返回
isnan	返回数组中的元素是否是一个 NaN，返回布尔型数组
isfinite, isinf	返回数组中的元素是否有限，是否无限，返回布尔型数组
cos, cosh, sin, sinh, tan, tanh	常规三角函数
arccos, arccosh, arcsin arcsinh, arctan, arctanh	常规反三角函数
logical_not	对数组的元素按位取反（与 ~arr 相等）

二元通用函数

函数名	描述
add	将数组的对应元素相加
subtract	将第一个数组逐元素减去第二个数组中的对应元素
multiply	将数组逐元素相乘
divide, floor_divide	除或乘除
power	将第一个数组的元素以其对应的第二个数组元素为次幂进行计算
maximum, fmax	逐个元素计算最大值，fmax 忽略 NaN
minimum, fmin	逐个元素计算最小值，fmin 忽略 NaN

二元通用函数

函数名	描述
mod	按元素的取模计算
copysign	将第一个数组的符号值改为第二个数组的符号值
greater, greater_equal less, less_equal equal, not_equal	同操作符 >, >=, <, <=, ==, !=
logical_and logical_or logical_xor	同操作符 &, 丨, ^

面向数组编程

面向数组编程

使用 NumPy 数组可以使你利用简单的数组表达式完成多种数组操作任务，而无须写大量循环。这种利用数组表达式来替代显示循环的方法，成为向量化。通常，向量化的数组操作回避纯 Python 的等价实现在速度上快一到两个数量级（甚至更多），这对所有种类的数值计算产生了很大的影响。np.where 函数是三元表达式 x if condition else y 的向量化版本，假设有如下数组：

xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
cond = np.array([True, False, True, True, False])

假设 cond 中的元素为 True 时，我们取 xarr 中的元素，否则取 yarr 中的元素，列式推导代码如下：

[(x if c else y) for x, y, c in zip(xarr,yarr,cond)]

[1.1, 2.2, 1.3, 1.4, 2.5]

当数组很大时，这种操作会很慢，同时当数组为多维时，就无法奏效了，np.where 代码如下：

np.where(cond, xarr, yarr)

array([1.1, 2.2, 1.3, 1.4, 2.5])

数学和统计方法

许多关于计算整个数组统计值或关于轴向数据的数学函数，可以作为数组类型的方法被调用。你可以使用聚合函数，比如 sum, mean 和 std，既可以使用数组实例的方法，也可以使用顶层的 NumPy 函数。

arr = np.random.randn(4, 3)
arr

array([[ 0.60047749, -1.21113259, -0.55198214],
       [ 2.06785396, -0.33324964, -2.04061021],
       [ 0.03179663, -0.77850557,  0.15115277],
       [ 1.60164335, -1.22691568, -0.99056909]])

arr.mean()

-0.22333672615328082

np.mean(arr)

-0.22333672615328082

arr.mean(axis=1)

array([-0.38754575, -0.10200196, -0.19851872, -0.20528047])

arr.sum(axis=0)

array([ 4.30177144, -3.54980348, -3.43200867])

统计方法

基础数组统计方法如下表所示：

函数名	描述
sum	沿着轴向计算所有元素的累加
mean	沿着轴向计算数学平均
std, var	标准差和方差，可以选择自由度
min, max	最小值和最大值
argmin, argmax	最小值和最大值的位置
cumsum	从 0 开始元素累积和
cumprod	从 1 开始元素累积积

排序

和 Python 内建列表类型相似，NumPy 数组可以使用 sort 方法按位置排序：

arr = np.random.randn(3)
arr

array([-1.42670524, -2.51592268, -0.53694831])

arr.sort()
arr

array([-2.51592268, -1.42670524, -0.53694831])

在多维数组中根据传的的 axis 值，沿着轴向对每个一维数据段进行排序：

arr = np.random.randn(3, 3)
arr

array([[-1.69826296, -1.02980194, -0.37991999],
       [ 0.39168133, -1.40975982, -0.01024077],
       [-0.10789377,  0.59755454, -0.19485425]])

arr.sort(1)
arr

array([[-1.69826296, -1.02980194, -0.37991999],
       [-1.40975982, -0.01024077,  0.39168133],
       [-0.19485425, -0.10789377,  0.59755454]])

顶层的 np.sort 方法返回的是已经排序好的数组拷贝，而不是对原数组按位置排序。

集合操作

NumPy 包含一些针对一维 ndarray 的基础集合操作，常用集合操作如下表所示：

函数名	描述
unique(x)	计算 x 的唯一值，并排序
intersect1d(x)	计算 x 和 y 的交集，并排序
union1d(x)	计算 x 和 y 的并集，并排序
in1d(x)	计算 x 中的元素是否包含在 y 中，返回一个布尔值数组
setdiff1d(x, y)	差集，在 x 中但不在 y 中的 x 的元素
setxor1d(x, y)	异或集，在 x 或 y 中，但不属于 x, y 交集的元素

线性代数

线性代数，例如矩阵乘法、分解、行列式等矩阵运算是所有数组类库的重要组成部分，常用线性代数函数如下表所示：

函数名	描述
diag	将一个方阵的对角元素作为一维数组返回，或将一维数组转换 成一个方阵，并将非对角线上的元素置为零
dot	矩阵点乘
trace	计算对角元素和
det	计算矩阵的行列式
eig	计算方阵的特征值和特征向量

线性代数

线性代数，例如矩阵乘法、分解、行列式等矩阵运算是所有数组类库的重要组成部分，常用线性代数函数如下表所示：

函数名	描述
inv	计算方阵的逆矩阵
pinv	计算矩阵的 Moore-Penrose 伪逆
qr	计算 QR 分解
svd	计算奇异值分解
solve	求解 \(x\) 的线性系统 \(Ax=b\) ，其中 \(A\) 是方阵
lstsq	计算 \(Ax=b\) 的最小二乘解

线性代数

np.random 填补了 Python 内建的 random 的不足，可以高效的生成多种概率分布下的数组，部分函数如下：

函数名	描述
seed	向随时数生成器传递随机数种子
permutation	返回一个序例的随机排列，或者返回一个乱序的整数范围序列
shuffle	随机排序一个序列
rand	从均匀分布中抽取样本
randint	根据给定的由低到高范围抽取随机整数
randn	从均值 0 方差 1 的正态分布中抽样样本（MATLAB 型接口）

函数名	描述
binomial	从二项分布中抽取样本
normal	从正态分布中抽取样本
beta	从 beta 分布中抽取样本
chisquare	从卡方分布中抽取样本
gamma	从伽马分布中抽取样本
uniform	从均匀分布 \(\left[0, 1\right)\) 中抽取样本

感谢倾听

本作品采用 授权

版权所有 © 范叶亮 Leo Van