特征工程

Feature Engineering

范叶亮 Leo Van

目录

• 数据预处理
• 特征变换和编码
• 特征提取，选择和监控

特征工程

在现实生活中，所有的事物都具有多种多样的属性（Attribute），例如：对于一个“人”，有性别，年龄，身高，体重等属性。在数据科学中，我们将一个所考察的对象的属性集合称之为特征（Feature）或特征集。特征工程（Feature Engineering）顾名思义是对特征进行一系列加工操作的过程，对于特征工程有多种不同的定义：

1. 特征工程是利用对数据的业务理解构建适合特定机器学习算法的特征的过程 ¹。
2. 特征工程是将原始数据转换成特征的过程。这些特征能够更好的将根本问题表达表述成预测模型，同时利用不可直接观测的数据提高模型准确性 ²。
3. 特征工程就是人工设计模型的输入变量 \(x\) 的过程 ³。

1. Wikipedia, “Feature engineering.” https://en.wikipedia.org/wiki/Feature_engineering

2. Brownlee, “Discover feature engineering, how to engineer features and how to get good at it.” http://machinelearningmastery.com/discover-feature-engineering-how-to-engineer-features-and-how-to-get-good-at-it/

3. T. Malisiewicz, “What is feature engineering?.” https://www.quora.com/What-is-feature-engineering

特征工程

从数据挖掘过程的角度，对“传统的”特征工程给出如下定义。特征工程就是指从原始数据（即通过现实生活中的实际业务发生产生的数据）加工得到最终用于特定的挖掘算法的输入变量的过程。此处之所以强调是“传统的”特征工程主要是用于区分其和近期基于深度学习等方法的自动特征生成。据此将特征工程划分为如下几个阶段：

• 数据预处理
• 特征变换和编码
• 特征提取和选择
• 特征监控

数据预处理

数据清洗

在实际的项目中，数据从生产和收集过程中往往由于机器或人的问题导致脏数据的生成，这些脏数据包括缺失，噪声，不一致等等一系列问题数据。脏数据的产生是不可避免的，但在后期的建模分析过程中，如果直接使用原始数据进行建模分析，则得到的结果会受到脏数据的影响从而表现很差。

• Data Cleaning
• Data Laundering
• Data Scrubbing
• Data Massaging

图片来源：https://xkcd.com/1838/

处理缺失值

对于数据缺失的情况，Rubin ¹ 从缺失机制的角度分为 3 类：完全随机缺失（missing completely at random，MCAR），随机缺失（missing at random）和非随机缺失（missing not at random，MNAR）。在 Missing Data ² 中定义有，对于一个数据集，变量 \(Y\) 存在数据缺失，如果 \(Y\) 的缺失不依赖于 \(Y\) 和数据集中其他的变量，称之为 MCAR。如果在控制其他变量的前提下，变量 \(Y\) 不依赖于 \(Y\) 本身，称之为 MAR，即：

\[ P \left(Y_{missing} | Y, X\right) = P \left(Y_{missing} | X\right) \]

如果上式不满足，则称之为 MNAR。例如：在一次人口调研中，我们分别收集了用户的年龄和收入信息，收入信息中存在缺失值，如果收入的缺失值仅依赖于年龄，则缺失值的类型为 MAR，如果收入的缺失值依赖于收入本身，则缺失值的类型为 MNAR。通过进一步分析，我们得到高收入者和低收入者在收入上的缺失率更高，因此收入的缺失类型属于 MNAR。

1. Rubin, Donald B. “Inference and missing data.” Biometrika 63.3 (1976): 581-592.

2. Allison, Paul D. Missing data. Vol. 136. Sage publications, 2001.

处理缺失值

缺失数据会在很多数据分析场景中出现，对于数值型数据，pandas 使用 NaN（Not a Number）表示缺失值:

s = pd.Series(
    ['aardvark', 'artichoke', np.nan, 'avocado']
)

s

0     aardvark
1    artichoke
2          NaN
3      avocado
dtype: object

s.isnull()

0    False
1    False
2     True
3    False
dtype: bool

pandas 中采用了 R 的编程惯例，将缺失值表示为 NA，意思是 not available。Python 内建的 None 值在对象数组中也被当作 NA：

s[0] = None
s.isnull()

0     True
1    False
2     True
3    False
dtype: bool

处理缺失值

在 Series 上通过 dropna 可以返回 Series 中所有的非空数据及其索引值：

from numpy import nan as NA

s = pd.Series([1, NA, 3.5, NA, 7])

s.dropna()

0    1.0
2    3.5
4    7.0
dtype: float64

s[s.notnull()]

0    1.0
2    3.5
4    7.0
dtype: float64

dropna 会删除所有包含缺失值的行：

df = pd.DataFrame(
    [[1., 6.5, 3.], [1., NA, NA], [NA, NA, NA], [NA, 6.5, 3]]
)

df

     0    1    2
0  1.0  6.5  3.0
1  1.0  NaN  NaN
2  NaN  NaN  NaN
3  NaN  6.5  3.0

df.dropna()

     0    1    2
0  1.0  6.5  3.0

df.dropna(how='all')

     0    1    2
0  1.0  6.5  3.0
1  1.0  NaN  NaN
3  NaN  6.5  3.0

处理缺失值

通过参数 axis=1 可以删除列：

df[4] = NA
df

     0    1    2   4
0  1.0  6.5  3.0 NaN
1  1.0  NaN  NaN NaN
2  NaN  NaN  NaN NaN
3  NaN  6.5  3.0 NaN

df.dropna(axis=1, how='all')

     0    1    2
0  1.0  6.5  3.0
1  1.0  NaN  NaN
2  NaN  NaN  NaN
3  NaN  6.5  3.0

通过 thresh 参数可以保留包含一定量数量的观察值：

df = pd.DataFrame(np.arange(9).reshape((3, 3)))
df.iloc[:2, 1] = NA
df.iloc[:1, 2] = NA
df

   0    1    2
0  0  NaN  NaN
1  3  NaN  5.0
2  6  7.0  8.0

df.dropna()

   0    1    2
2  6  7.0  8.0

df.dropna(thresh=2)

   0    1    2
1  3  NaN  5.0
2  6  7.0  8.0

补全缺失值

pandas 中利用 fillna 方法可以补全缺失值：

df.fillna(0)

   0    1    2
0  0  0.0  0.0
1  3  0.0  5.0
2  6  7.0  8.0

使用字典值可以为不同列填充不同值：

df.fillna({1: 0.5, 2: 0})

   0    1    2
0  0  0.5  0.0
1  3  0.5  5.0
2  6  7.0  8.0

fillna 函数参数如下表所示：

参数	描述
value	标量值或字典型对象用于填充缺失值
method	插值方法，如果没有其他参数，默认是 ffill
axis	需要填充的轴，默认 axis=0
inplace	是否就地填充
limit	用于向前或向后填充时最大的填充范围

补全缺失值

利用 scikit-learn 中的 impute.SimpleImputer, impute.IterativeImputer 和 impute.KNNImputer 可以进行单变量，多变量和基于 KNN 的缺失值补全。

sklearn.impute.SimpleImputer(
    *, missing_values=nan, strategy='mean', fill_value=None, copy=True, add_indicator=False,
    keep_empty_features=False)

sklearn.impute.IterativeImputer(
    estimator=None, *, missing_values=nan, sample_posterior=False, max_iter=10, tol=0.001, n_nearest_features=None,
    initial_strategy='mean', fill_value=None, imputation_order='ascending', skip_complete=False,
    min_value=-inf, max_value=inf, verbose=0, random_state=None, add_indicator=False, keep_empty_features=False)

sklearn.impute.KNNImputer(
    *, missing_values=nan, n_neighbors=5, weights='uniform', metric='nan_euclidean', copy=True, add_indicator=False,
    keep_empty_features=False)

实例方法有：fit(self, X[, y])（拟合数据），fit_transform(self, X[, y])（拟合并补全数据），get_params(self[, deep])（获取参数），set_params(self, **params)（设置参数），transform(self, X)（补全数据）。

补全缺失值

参数	说明
missing_values	缺失值
strategy	填补策略：mean, median, most_frequent, constant
fill_value	填补值
copy	是否拷贝新对象
estimator	用于每一轮 round-robin 补全的估计器
sample_posterior	是否从拟合估计量的预测后验值中对每次估算进行抽样
max_iter	最大迭代次数
tol	停止准则

补全缺失值

参数	说明
n_nearest_features	用于估计缺失值的特征个数
initial_strategy	初始策略，同 strategy
imputation_order	填补顺序 ascending, descending, roman, arabic, random
n_neighbors	用于估计缺失值的邻居个数
weights	预测时的权重函数 uniform, distance 或自定义函数
metric	搜寻邻居的距离度量 nan_euclidean 或自定义函数

单变量补全缺失值

from sklearn.impute import SimpleImputer

imp_mean = SimpleImputer(missing_values=np.nan, strategy='mean')
imp_mean.fit([[7, 2, 3], [4, np.nan, 6], [10, 5, 9]])

SimpleImputer()

X = [[np.nan, 2, 3], [4, np.nan, 6], [10, np.nan, 9]]
imp_mean.transform(X)

array([[ 7. ,  2. ,  3. ],
       [ 4. ,  3.5,  6. ],
       [10. ,  3.5,  9. ]])

多变量补全缺失值

from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer

imp_mean = IterativeImputer(random_state=0)
imp_mean.fit([[7, 2, 3], [4, np.nan, 6], [10, 5, 9]])

IterativeImputer(random_state=0)

X = [[np.nan, 2, 3], [4, np.nan, 6], [10, np.nan, 9]]
imp_mean.transform(X)

array([[ 6.95847623,  2.        ,  3.        ],
       [ 4.        ,  2.6000004 ,  6.        ],
       [10.        ,  4.99999933,  9.        ]])

KNN 补全缺失值

from sklearn.impute import KNNImputer

X = [[1, 2, np.nan], [3, 4, 3], [np.nan, 6, 5], [8, 8, 7]]
imputer = KNNImputer(n_neighbors=2)
imputer.fit_transform(X)

array([[1. , 2. , 4. ],
       [3. , 4. , 3. ],
       [5.5, 6. , 5. ],
       [8. , 8. , 7. ]])

删除重复值

去重是指对于数据中重复的部分进行删除操作，对于一个数据集，可以从“样本”和“特征”两个角度去考虑重复的问题。

样本去重：从“样本”的角度，相同的事件或样本（即所有特征的值均一致）重复出现是可能发生的。但从业务理解的角度上考虑，并不是所有的情况都允许出现重复样本，例如：我们考察一个班级的学生其平时表现和最终考试成绩之间的相关性时，假设利用学号作为学生的唯一标识，则不可能存在两个学号完全相同的学生。则这种情况下我们就需要对于重复的“样本”做出取舍。

特征去重：从“特征”的角度，不同的特征在数值上有差异，但其背后表达的物理含义可能是相同的。例如：一个人的月均收入和年收入两个特征，尽管在数值上不同，但其表达的都是一个人在一年内的收入能力，两个特征仅相差常数倍。因此，对于仅相差常数倍的特征需要进行去重处理，保留任意一个特征即可。

常量特征剔除：对于常量或方差近似为零的特征，其对于样本之间的区分度贡献为零或近似为零，这些特征对于后面的建模分析没有任何意义。

删除重复值

在 DataFrame 中，会出现重复值，duplicated 函数会返回一个布尔值 Series 用于标注每一行是否存在重复：

df = pd.DataFrame({
    'k1': ['one', 'two'] * 3 + ['two'],
    'k2': [1, 1, 2, 3, 3, 4, 4]})

df

    k1  k2
0  one   1
1  two   1
2  one   2
3  two   3
4  one   3
5  two   4
6  two   4

df.duplicated()

0    False
1    False
2    False
3    False
4    False
5    False
6     True
dtype: bool

drop_duplicates 返回的是 DataFrame，内容是 duplicated 返回数组中为 False 的部分：

df.drop_duplicates()

    k1  k2
0  one   1
1  two   1
2  one   2
3  two   3
4  one   3
5  two   4

df.drop_duplicates(['k1'])

    k1  k2
0  one   1
1  two   1

duplicated 和 drop_duplicates 默认都是保留第一个观测到的值。传入 keep='last' 将会保留最后一个。

异常值处理

异常值是指样本中存在的同样本整体差异较大的数据，异常数据可以划分为两类：

1. 异常值不属于该总体，而是从另一个总体错误抽样到样本中而导致的较大差异。
2. 异常值属于该总体，是由于总体所固有的变异性而导致的较大差异。

对于数值型的单变量，我们可以利用拉依达准则对其异常值进行检测。假设总体 \(x\) 服从正态分布，则：

\[ P\left(|x - \mu| > 3 \sigma\right) \leq 0.003 \]

其中 \(\mu\) 表示总体的期望，\(\sigma\) 表示总体的标准差。因此，对于样本中出现大于 \(\mu + 3\sigma\) 或小于 \(\mu - 3\sigma\) 的数据的概率是非常小的，从而可以对大于 \(\mu + 3\sigma\) 或小于 \(\mu - 3\sigma\) 的数据予以剔除。

异常值处理

异常检测（Anomaly Detection）是指对不符合预期模式或数据集中异常项目、事件或观测值的识别。通常异常的样本可能会导致银行欺诈、结构缺陷、医疗问题、文本错误等不同类型的问题。异常也被称为离群值、噪声、偏差和例外。

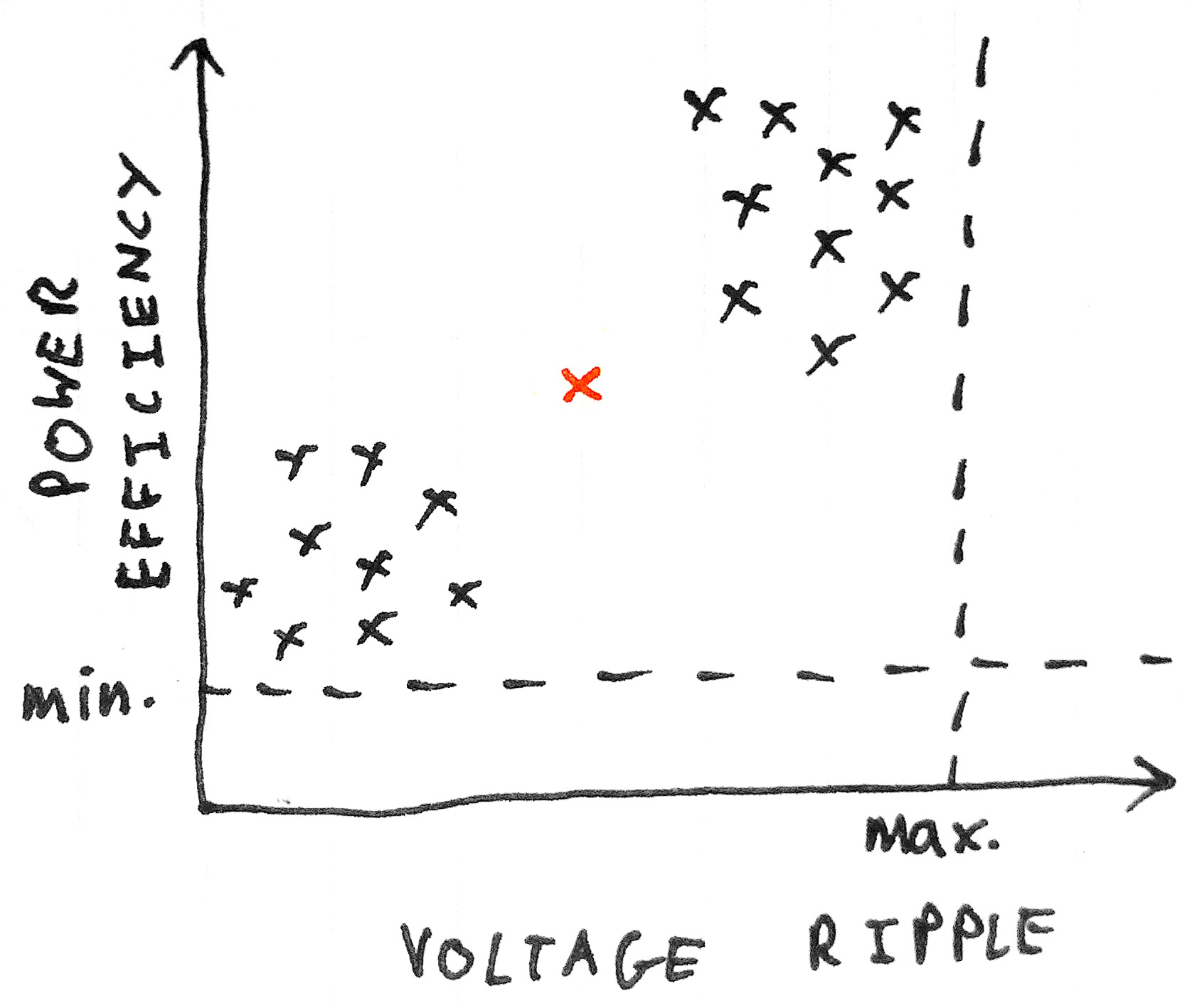
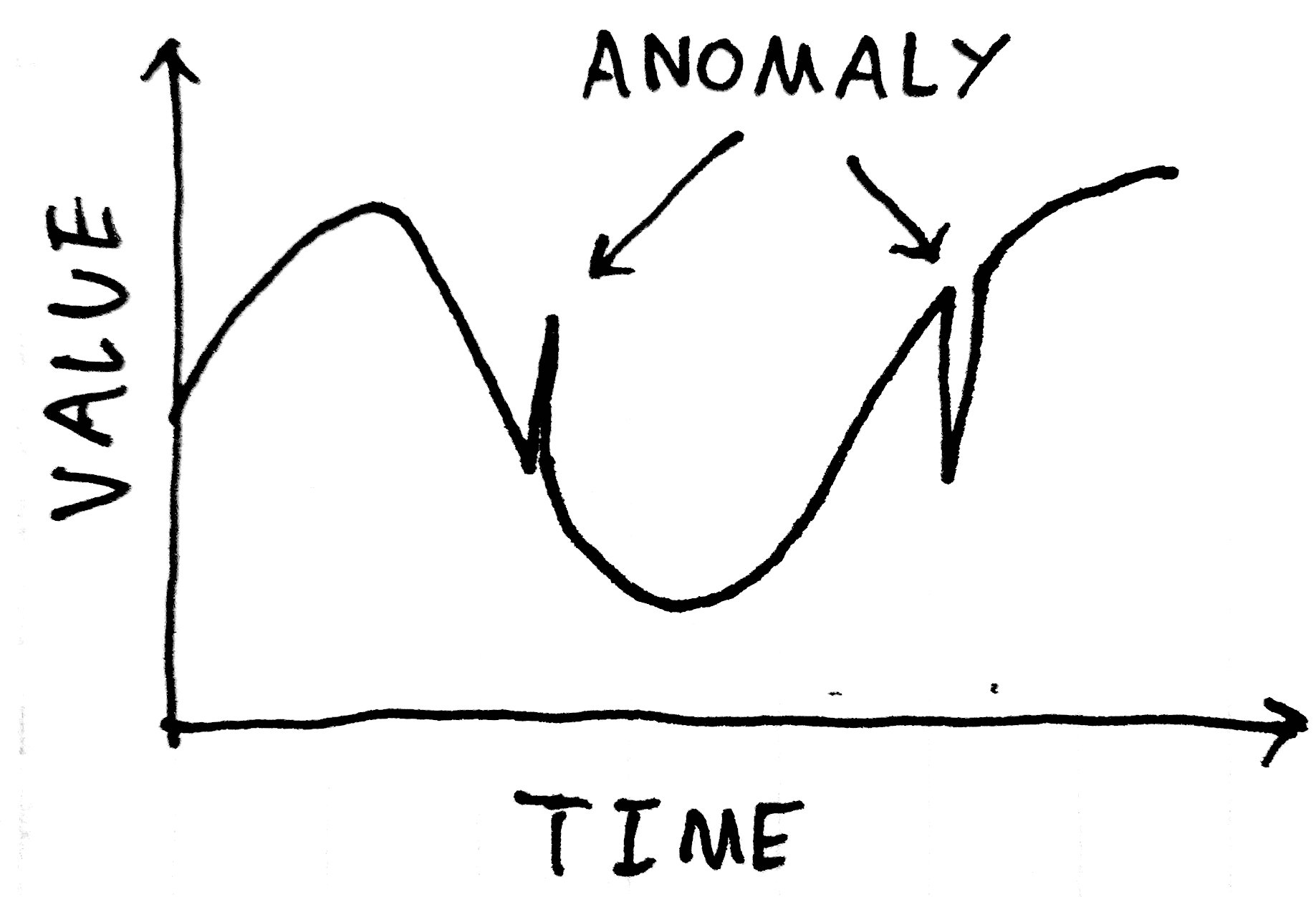
异常检测

异常检测技术用于各种领域，如入侵检测、欺诈检测、故障检测、系统健康监测、传感器网络事件检测和生态系统干扰检测等。它通常用于在预处理中删除从数据集的异常数据。在监督式学习中，去除异常数据的数据集往往会在统计上显著提升准确性。

常用的异常检测算法有：

• 基于密度的方法：最近邻居法、局部异常因子等
• One-Class SVM
• 基于聚类的方法
• Isolation Forest
• AutoEncoder

图片来源：https://scikit-learn.org/stable/modules/outlier_detection.html

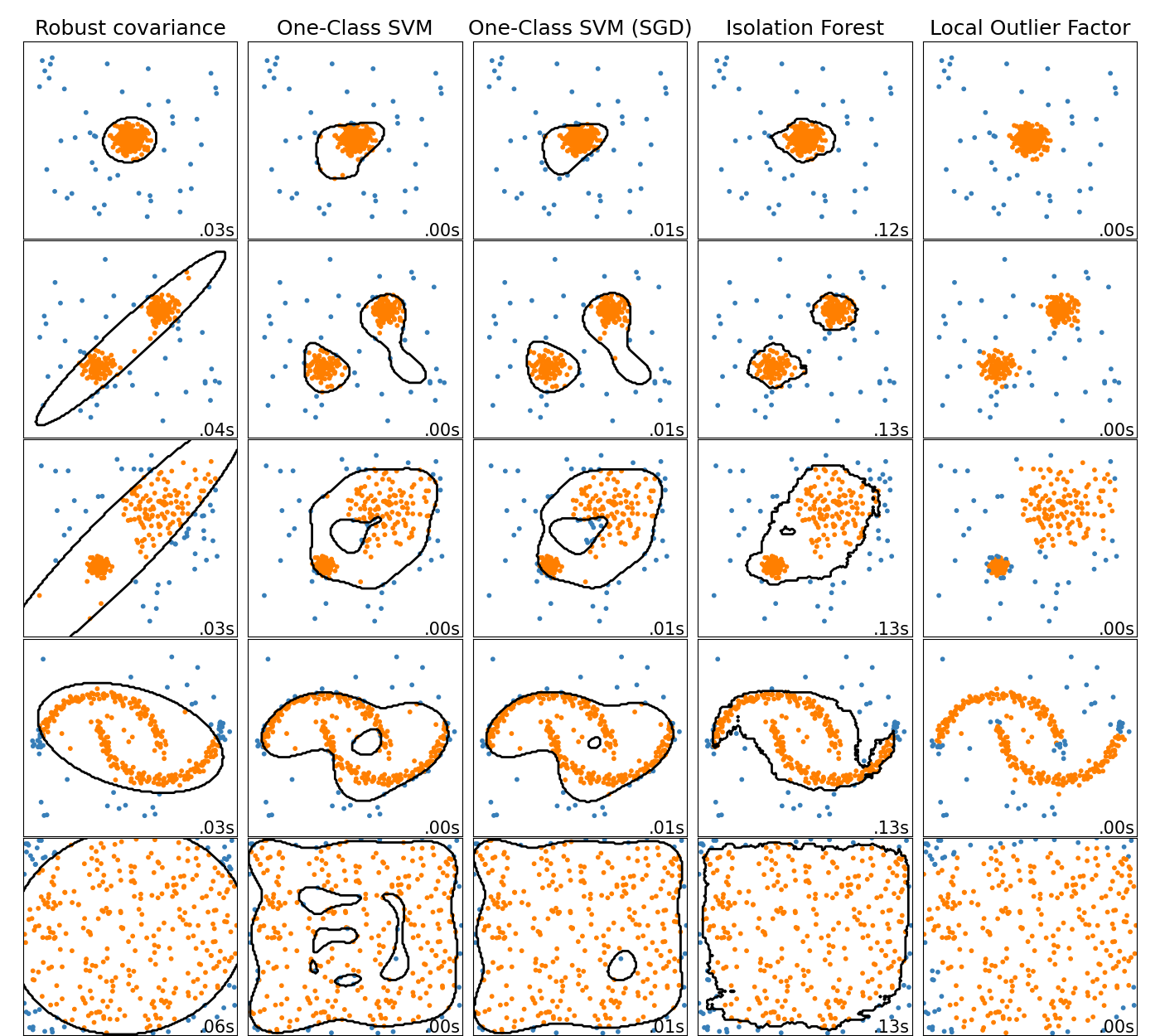
异常检测

箱线图（Boxplot），是利用数据中的五个统计量：最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法，它也可以粗略地看出数据是否具有有对称性，分布的分散程度等信息。

\[ \begin{split} LowerLimit &= \max \{Q_1 - 1.5 * IQR, Minimum\} \\ UpperLimit &= \min \{Q_3 + 1.5 * IQR, Maximum\} \\ IQR &= Q_3 - Q_1 \end{split} \]

异常检测

Isolation Forest，Isolation 意为孤立、隔离，是名词，Forest 是森林，合起来就是“孤立森林”了，也有叫“独异森林”，并没有统一的中文叫法，大家更习惯用其英文的名字 isolation forest，简称 iForest ^{1 2}。

iForest 算法用于挖掘异常数据，或者说离群点挖掘，总之是在一大堆数据中，找出与其它数据的规律不太符合的数据。通常用于网络安全中的攻击检测和流量异常等分析，金融机构则用于挖掘出欺诈行为。对于找出的异常数据，然后要么直接清除异常数据，如数据清理中的去除噪声数据，要么深入分析异常数据，比如分析攻击、欺诈的行为特征。

1. Liu, Fei Tony, Kai Ming Ting, and Zhi-Hua Zhou. “Isolation forest.” 2008 Eighth IEEE International Conference on Data Mining. IEEE, 2008.

2. Liu, Fei Tony, Kai Ming Ting, and Zhi-Hua Zhou. “Isolation-based anomaly detection.” ACM Transactions on Knowledge Discovery from Data (TKDD) 6.1 (2012): 1-39.

异常检测

iForest 属于非监督学习的方法，假设我们用一个随机超平面来切割数据空间，切一次可以生成两个子空间。之后我们再继续用一个随机超平面来切割每个子空间，循环下去，直到每子空间里面只有一个数据点为止。iForest 由 \(t\) 个 iTree（Isolation Tree）孤立树组成，每个 iTree 是一个二叉树结构，其实现步骤如下：

1. 从训练集中随机选择 \(\phi\) 个点样本点，放入树的根节点。
2. 随机指定一个特征，在当前节点数据中随机产生一个切割点 \(p\)，切割点产生于当前节点数据中指定维度的最大值和最小值之间。
3. 以此切割点生成了一个超平面，将当前数据空间划分为 2 个子空间：小于 \(p\) 的数据作为当前节点的左孩子，大于等于 \(p\) 的数据作为当前节点的右孩子。
4. 在孩子节点中递归步骤 2 和 3，不断构造新的孩子节点，直到孩子节点只有一个数据或孩子节点已到达限定高度。

获得 \(t\) 个 iTree 之后，iForest 训练就结束，然后我们可以用生成的 iForest 来评估测试数据了。对于一个训练数据 \(x\)，我们令其遍历每一棵 iTree，然后计算 \(x\) 最终落在每个树第几层。然后我们可以得出 \(x\) 在每棵树的高度平均值。获得每个测试数据的平均深度后，我们可以设置一个阈值，其平均深度小于此阈值的即为异常。

异常检测

sklearn.ensemble.IsolationForest(
    *, n_estimators=100, max_samples='auto',
    contamination='auto', max_features=1.0,
    bootstrap=False, n_jobs=None, random_state=None,
    verbose=0, warm_start=False)

from sklearn.ensemble import IsolationForest

X = np.array([
    [-1, -1], [-2, -1], [-3, -2],
    [0, 0], [-20, 50], [3, 5]]
)
clf = IsolationForest(
    n_estimators=10, warm_start=True).fit(X)
clf.predict(X)

array([ 1,  1,  1,  1, -1, -1])

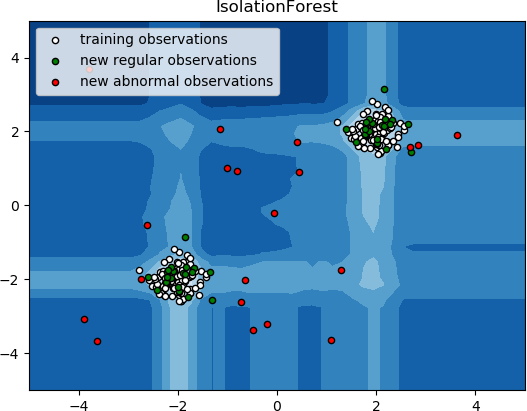
数据采样

简单随机抽样：从总体 \(N\) 个单位中随机地抽取 \(n\) 个单位作为样本，使得每一个容量为样本都有相同的概率被抽中。特点是：每个样本单位被抽中的概率相等，样本的每个单位完全独立，彼此间无一定的关联性和排斥性。

分层抽样：将抽样单位按某种特征或某种规则划分为不同的层，然后从不同的层中独立、随机地抽取样本。从而保证样本的结构与总体的结构比较相近，从而提高估计的精度。

欠采样和过采样：在处理有监督的学习问题的时候，我们经常会碰到不同分类的样本比例相差较大的问题，这种问题会对我们构建模型造成很大的影响，因此从数据角度出发，我们可以利用欠采样或过采样处理这种现象。

数据采样

利用 Series 和 DataFrame 的 sample 方法可以进行随机抽样：

df = pd.DataFrame(np.arange(5 * 4).reshape((5, 4)))

df

    0   1   2   3
0   0   1   2   3
1   4   5   6   7
2   8   9  10  11
3  12  13  14  15
4  16  17  18  19

df.sample(n=3)

    0   1   2   3
2   8   9  10  11
1   4   5   6   7
3  12  13  14  15

通过设置参数 replace=True 可以进行有重复的采样：

s = pd.Series([5, 7, -1, 6, 4])
s.sample(n=10, replace=True)

3    6
3    6
2   -1
3    6
2   -1
2   -1
1    7
0    5
4    4
3    6
dtype: int64

数据集分割

将数据分割为训练集和测试集的目的是要确保机器学习算法可以从中获得有用价值的信息。因此没必要将太多信息分配给测试集。然而，测试集越小，泛化误差的估计就越不准确。将数据集分割为训练集和测试集就是对两者的平衡。

在实践中，最常用的分割比例为 60:40，70:30，80:20，具体取决于数据集的规模，对于大数据集分割比例为 90:10 或 99:1 也是常见和适当的做法。

一般的做法是在模型训练和评估后保留测试数据，然后在整个数据集上再进行训练，以提高模型的性能。虽然通常推荐这种做法，但它可能会导致较差的泛化性能。

sklearn.model_selection.train_test_split(
    *arrays, **options)

参数	描述
*array	具有相同长度或 shape[0] 的数据
test_size	测试集比例
train_size	训练集比例
random_state	随机数种子
shuffle	是否对数据进行混排
stratify	分层所需的类标签

数据集分割

from sklearn.model_selection import train_test_split

X, y = np.arange(10).reshape((5, 2)), range(5)

X

array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7],
       [8, 9]])

y

range(0, 5)

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=42)

X_train

array([[4, 5],
       [0, 1],
       [6, 7]])

y_train

[2, 0, 3]

X_test

array([[2, 3],
       [8, 9]])

y_test

[1, 4]

train_test_split(y, shuffle=False)

[[0, 1, 2], [3, 4]]

特征变换和编码

无量纲化

归一化一般是指将数据的取值范围缩放到 \(\left[0, 1\right]\) 之间，当然部分问题也可能会缩放到 \(\left[-1, 1\right]\) 之间。针对一般的情况，归一化的结果可以表示为：

\[ x' = \dfrac{x - x_{\min}}{x_{\max} - x_{\min}} \]

其中，\(x_{\min}\) 表示 \(x\) 中的最小值，\(x_{\max}\) 表示 \(x\) 中的最大值。

通过归一化，我们可以消除不同量纲下的数据对最终结果的影响。例如，我们通过身高（单位：米）和体重（单位：公斤）来衡量两个人之间的差异，两个人的的体重相差 20 公斤，身高相差 0.1 米，因此在这样的量纲下衡量这两个人的差异时，体重的差异会把身高的差异遮盖掉，但这往往不是我们想要的结果。但通例如我们假设体重的最小值和最大值分别为 0 和 200 公斤，身高的最小值和最大值分别为 0 和 2 米，因此归一化后体重和身高的差距变为 0.1 和 0.05，因此通过归一下则可以避免这样的问题的出现。

无量纲化

sklearn.preprocessing.MinMaxScaler(feature_range=(0, 1), *, copy=True, clip=False)

from sklearn.preprocessing import MinMaxScaler

data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
scaler = MinMaxScaler()
scaler.fit(data)

MinMaxScaler()

scaler.data_max_

array([ 1., 18.])

scaler.transform(data)

array([[0.  , 0.  ],
       [0.25, 0.25],
       [0.5 , 0.5 ],
       [1.  , 1.  ]])

scaler.transform([[2, 2]])

array([[1.5, 0. ]])

无量纲化

标准化的目的是为了让数据的均值为 0，标准差为 1，标准化还称为 Z-score，标准化的结果可以表示为 \(x' = \dfrac{x - \overline{X}}{S}\)，其中，\(\overline{X}\) 为 \(x\) 的均值，\(S\) 为 \(x\) 的标准差。

sklearn.preprocessing.StandardScaler(*, copy=True, with_mean=True, with_std=True)

from sklearn.preprocessing import StandardScaler
data = [[0, 0], [0, 0], [1, 1], [1, 1]]
scaler = StandardScaler()
scaler.fit(data)

StandardScaler()

scaler.mean_

array([0.5, 0.5])

scaler.transform(data)

array([[-1., -1.],
       [-1., -1.],
       [ 1.,  1.],
       [ 1.,  1.]])

scaler.transform([[2, 2]])

array([[3., 3.]])

无量纲化

通过标准化得到的新的数据均值为 0 和标准差为 1 的新特征，这些新特征在后续处理中会有很多好处。例如：我们将标准差统一到 1，从信息论角度，方差可以表示其中蕴含的信息量越大，信息量越大对模型的影响就也大，因此我们将其标准化到 1，这样就消除了最开始不同变量具有不同的影响程度的差异。

除此之外，去量纲化在利用梯度下降等方法求最优解的时候也具有重要的作用。在利用梯度下降等方法求最优解的时候，每次我们都会朝着梯度下降的最大方向迈出一步，但当数据未经过去量纲化的原始数据时，每次求解得到的梯度方向可能和真实的误差最小的方向差异较大，这样就会可能导致收敛的速度很慢甚至无法收敛。而通过去量纲化后的数据，其目标函数会变得更“圆”，此时每一步梯度的方向和真实误差最小的方向的偏差就会比较小，模型就可以很快收敛到误差最小的地方。

分箱

分箱是一种数据预处理技术，用于减少次要观察误差的影响，是一种将多个连续值分组为较少数量的“分箱”的方法。分箱的一些优势如下：

• 离散化后的特征对异常数据有更强的鲁棒性。
• 逻辑回归属于广义线性模型，表达能力受限，单变量离散化为 \(N\) 个后，每个变量有单独的权重，为模型引入了非线性，提升模型表达能力，加大拟合。
• 离散化后可以进行特征交叉，由 \(M + N\) 个变量变为 \(M \times N\) 个变量，进一步引入非线性提升表达能力。
• 可以将缺失作为独立的一类带入模型。
• 将所有变量变换到相似的尺度上。

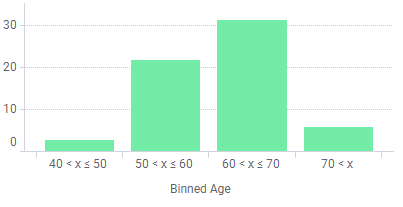
分箱

sklearn.preprocessing.KBinsDiscretizer(
    n_bins=5, *, encode='onehot', strategy='quantile', quantile_method='warn', dtype=None, subsample=200000,
    random_state=None)

其中，n_bins 表示分箱个数，encode 表示编码方式（'onehot'：One-Hot 编码稀疏矩阵，'onehot-dense'：One-Hot 编码稠密矩阵，'ordinal'：分箱整数标识值），strategy 表示分箱方法（'uniform'：等宽分箱，'quantile'：等深分箱，'kmeans'：K-means 方法）。

from sklearn.preprocessing import \
    KBinsDiscretizer

X = [[-2, 1, -4,   -1],
    [-1, 2, -3, -0.5],
    [ 0, 3, -2,  0.5],
    [ 1, 4, -1,    2]]

est = KBinsDiscretizer(
    n_bins=3, encode='ordinal',
    strategy='uniform')

est.fit(X)

KBinsDiscretizer(encode='ordinal', n_bins=3, strategy='uniform')

Xt = est.transform(X)
Xt

array([[0., 0., 0., 0.],
       [1., 1., 1., 0.],
       [2., 2., 2., 1.],
       [2., 2., 2., 2.]])

est.bin_edges_[0]

array([-2., -1.,  0.,  1.])

est.inverse_transform(Xt)

array([[-1.5,  1.5, -3.5, -0.5],
       [-0.5,  2.5, -2.5, -0.5],
       [ 0.5,  3.5, -1.5,  0.5],
       [ 0.5,  3.5, -1.5,  1.5]])

分类标签编码

很多机器学习库要求分类标签的编码为整数值，可以利用 sklearn.preprocessing 中的 LabelBinarizer，MultiLabelBinarizer 和 LabelEncoder 实现。

sklearn.preprocessing.LabelBinarizer(*, neg_label=0, pos_label=1, sparse_output=False)
sklearn.preprocessing.MultiLabelBinarizer(*, classes=None, sparse_output=False)

from sklearn.preprocessing import \
    LabelBinarizer, MultiLabelBinarizer
lb = LabelBinarizer()
lb.fit([1, 2, 6, 4, 2])

LabelBinarizer()

lb.classes_

array([1, 2, 4, 6])

lb.transform([1, 6])

array([[1, 0, 0, 0],
       [0, 0, 0, 1]])

mlb = MultiLabelBinarizer()
mlb.fit_transform([(1, 2), (3,)])

array([[1, 1, 0],
       [0, 0, 1]])

分类标签编码

sklearn.preprocessing.LabelEncoder()

from sklearn.preprocessing import LabelEncoder

le = LabelEncoder()
le.fit([1, 2, 2, 6])

LabelEncoder()

le.classes_

array([1, 2, 6])

le.transform([1, 1, 2, 6])

array([0, 0, 1, 2])

le.inverse_transform([0, 0, 1, 2])

array([1, 1, 2, 6])

le.fit(['paris', 'paris', 'tokyo', 'amsterdam'])

LabelEncoder()

le.classes_

array(['amsterdam', 'paris', 'tokyo'], dtype='<U9')

le.transform(['tokyo', 'tokyo', 'paris'])

array([2, 2, 1])

One-Hot 编码

对于多个分类，将其编码为整数后默认引入了之前大小差异的假设，例如：blue=0, green=1, red=2，blue 和 green 之间相差 1，但 blue 和 red 之间相差 2，但实际上三者之间的差异应该是相同的。为了解决这个问题，我们可以采用 One-Hot 编码，其将一个特征表示为 \(N\) 维向量， \(N\) 为特征类型个数，向量每一位为 \(0\) 或 \(1\)。我们可以利用 pandas 中的 get_dummies 方法获取编码后的特征，使用 One-Hot 编码时需要注意可能带来的多重共线性，通过设置 drop_first=True 可以删除第一列从而避免该问题。

df = pd.DataFrame({
    'size': [1, 2, 3],
    'color': ['blue', 'green', 'red']})
df

   size  color
0     1   blue
1     2  green
2     3    red

pd.get_dummies(df)

   size  color_blue  color_green  color_red
0     1        True        False      False
1     2       False         True      False
2     3       False        False       True

pd.get_dummies(df, drop_first=True)

   size  color_green  color_red
0     1        False      False
1     2         True      False
2     3        False       True

One-Hot 编码

sklearn.preprocessing.OneHotEncoder(
    *, categories='auto', drop=None, sparse_output=True, dtype=numpy.float64, handle_unknown='error',
    min_frequency=None, max_categories=None, feature_name_combiner='concat')

from sklearn.preprocessing import OneHotEncoder
X = [['blue'], ['green'], ['red']]
enc = OneHotEncoder(handle_unknown='ignore').fit(X)
enc.categories_

[array(['blue', 'green', 'red'], dtype=object)]

enc.transform([['red']]).toarray()

array([[0., 0., 1.]])

enc.inverse_transform([[0, 1, 0], [0, 0, 0]])

array([['green'],
       [None]], dtype=object)

enc.get_feature_names_out(['color'])

array(['color_blue', 'color_green', 'color_red'], dtype=object)

drop_enc = OneHotEncoder(drop='first').fit(X)
drop_enc.categories_

[array(['blue', 'green', 'red'], dtype=object)]

drop_enc.transform([['red']]).toarray()

array([[0., 1.]])

特征提取，选择和监控

特征提取

• 人工特征提取
  • SQL
  • SQL
  • SQL
• 降维
  • 主成分分析
  • 线性判别分析
  • 多维标度法
  • 等距映射算法
  • 局部线性嵌入
  • 流行学习 ¹：SNE，t-SNE，LargeVis

• 表示学习
  • 文本，图像，序列…
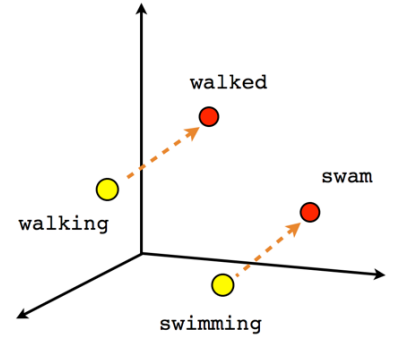
  • Something2Vec ²

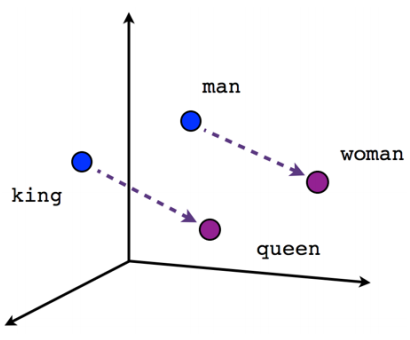
King - Man + Woman = Queen
Walking - Wakled + Swam = Swimmming

1. https://leovan.me/cn/2018/03/manifold-learning/

2. https://gist.github.com/nzw0301/333afc00bd508501268fa7bf40cafe4e

主成分分析

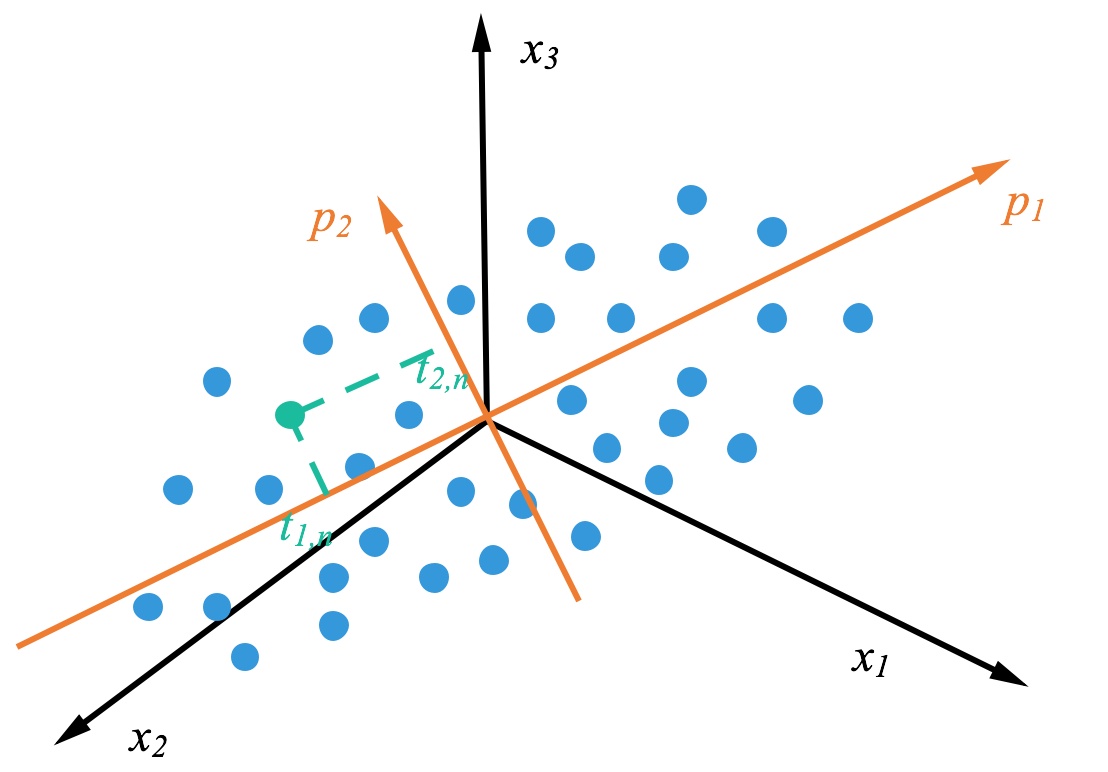
主成分分析（Principal Components Analysis，PCA）由 Pearson ¹ 于 1901 年提出。主成分分析可以将多个相关变量转化为少数几个不相关变量的统计分析方法。通过主成分分析 PCA 量保留原始信息的基础上，尽可能提出更少的不相关变量（主成分），可以对数据进行有效的降维。

右图是 PCA 的投影的一个表示，蓝色的点是原始的点，带箭头的橘黄色的线是投影的向量，\(p_1\) 表示特征值最大的特征向量，\(p_2\) 表示特征值次大的特征向量。

1. Pearson, Karl. “LIII. On lines and planes of closest fit to systems of points in space.” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 2.11 (1901): 559-572.

主成分分析

主成分分析 ¹ 可以通俗的理解为一种降维方法。其目标可以理解为将一个 \(m\) 维的数据转换称一个 \(k\) 维的数据，其中 \(k < m\)。对于具有 \(n\) 个样本的数据集，设 \(\boldsymbol{x_i}\) 表示 \(m\) 维的列向量，则

\[ X_{m*n} = \left(\boldsymbol{x_1}, \boldsymbol{x_2}, ..., \boldsymbol{x_n}\right) \]

对每一个维度进行零均值化，即减去这一维度的均值

\[ X'_{m*n} = X - \boldsymbol{u}\boldsymbol{h} \]

其中，\(\boldsymbol{u}\) 是一个 \(m\) 维的行向量，\(\boldsymbol{u}[m] = \dfrac{1}{n} \sum_{i=1}^{n} X[m, i]\)；\(h\) 是一个值全为 \(1\) 的 \(n\) 维行向量。

1. Wold, Svante, Kim Esbensen, and Paul Geladi. “Principal component analysis.” Chemometrics and intelligent laboratory systems 2.1-3 (1987): 37-52.

主成分分析

对于两个随机变量，我们可以利用协方差简单表示这两个变量之间的相关性

\[ \text{cov} \left(x, y\right) = E \left(\left(x - \mu_x\right) \left(y - \mu_y\right)\right) \]

对于已经零均值化后的矩阵 \(X'\)，计算得出如下矩阵：

\[ C = \dfrac{1}{n} X' X'^{\top} = \left\lgroup \begin{array}{cccc} \dfrac{1}{n} \sum_{i=1}^{n} x_{1i}^2 & \dfrac{1}{n} \sum_{i=1}^{n} x_{1i} x_{2i} & \cdots & \dfrac{1}{n} \sum_{}^{} x_{1i} x_{ni} \\ \dfrac{1}{n} \sum_{i=1}^{n} x_{2i} x_{1i} & \dfrac{1}{n} \sum_{i=1}^{n} x_{2i}^2 & \cdots & \dfrac{1}{n} \sum_{}^{} x_{2i} x_{ni} \\ \vdots & \vdots & & \vdots \\ \dfrac{1}{n} \sum_{i=1}^{n} x_{mi} x_{1i} & \dfrac{1}{n} \sum_{i=1}^{n} x_{mi} x_{2i} & \cdots & \dfrac{1}{n} \sum_{}^{} x_{mi}^2 \\ \end{array} \right\rgroup \]

因为矩阵 \(X'\) 已经经过了零均值化处理，因此矩阵 \(C\) 中对角线上的元素为维度 \(m\) 的方差，其他元素则为两个维度之间的协方差。从 PCA 的目标来看，我们则可以通过求解矩阵 \(C\) 的特征值和特征向量，将其特征值按照从大到小的顺序按行重排其对应的特征向量，则取前 \(k\) 个，则实现了数据从 \(m\) 维降至 \(k\) 维。

主成分分析

sklearn.decomposition.PCA(
    n_components=None, *, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto',
    n_oversamples=10, power_iteration_normalizer='auto', random_state=None)

参数	描述
n_components	保留的成分个数
copy	如果为 False，使用 fit_transform(X) 获得结果，fit(X).transform(X) 并不会获得预期结果
whiten	是否进行白化
svd_solver	SVD 求解器，auto, full, covariance_eigh, arpack, randomized
tol	当 svd_solver='arpack' 时奇异值的惩罚项

主成分分析

from sklearn.decomposition import PCA

X = np.array([
    [-1, -1], [-2, -1], [-3, -2],
    [1, 1], [2, 1], [3, 2]])

pca = PCA(n_components=2).fit(X)
pca.explained_variance_ratio_

array([0.99244289, 0.00755711])

pca.singular_values_

array([6.30061232, 0.54980396])

pca = PCA(n_components=1, svd_solver='arpack')
pca.fit(X)

PCA(n_components=1, svd_solver='arpack')

pca.explained_variance_ratio_

array([0.99244289])

pca.singular_values_

array([6.30061232])

特征选择

特征选择本质上继承了奥卡姆剃刀的思想，从一组特征中选出一些最有效的特征，使构造出来的模型更好。

• 避免过度拟合，改进预测性能
• 使学习器运行更快，效能更高
• 剔除不相关的特征使模型更为简单，容易解释

过滤方法（Filter Methods）：按照发散性或相关性对特征进行评分，设定阈值或者待选择阈值的个数，选择特征。

• 方差选择法：选择方差大的特征。
• 相关关系 & 卡方检验：特征与目标值的相关关系。
• 互信息法：一个随机变量包含另一个随机变量的信息量。

特征选择

封装方法（Wrapper Methods）：是利用学习算法的性能来评价特征子集的优劣。因此，对于一个待评价的特征子集，Wrapper 方法需要训练一个分类器，根据分类器的性能对该特征子集进行评价，学习算法包括决策树、神经网络、贝叶斯分类器、近邻法以及支持向量机等。Wrapper 方法缺点主要是特征通用性不强，当改变学习算法时，需要针对该学习算法重新进行特征选择。

集成方法（Embedded Methods）：在集成法特征选择中，特征选择算法本身作为组成部分嵌入到学习算法里。最典型的即决策树算法。包括基于惩罚项的特征选择法和基于树模型的特征选择法。

特征选择

from sklearn.feature_selection import \
    VarianceThreshold

X = [[0, 0, 1], [0, 1, 0], [1, 0, 0],
    [0, 1, 1], [0, 1, 0], [0, 1, 1]]
sel = VarianceThreshold(threshold=(.8 * (1 - .8)))
sel.fit_transform(X)

array([[0, 1],
       [1, 0],
       [0, 0],
       [1, 1],
       [1, 0],
       [1, 1]])

from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

X, y = load_iris(return_X_y=True)
X.shape

(150, 4)

X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
X_new.shape

(150, 2)

特征选择

from sklearn.svm import LinearSVC
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.feature_selection import \
    SelectFromModel

X, y = load_iris(return_X_y=True)
X.shape

(150, 4)

lsvc = LinearSVC(
    C=0.01, penalty='l1', dual=False).fit(X, y)
model = SelectFromModel(lsvc, prefit=True)
X_new = model.transform(X)
X_new.shape

(150, 3)

X, y = load_iris(return_X_y=True)
X.shape

(150, 4)

clf = ExtraTreesClassifier(n_estimators=50).fit(X, y)
clf.feature_importances_

array([0.13256884, 0.04989539, 0.38696912, 0.43056665])

model = SelectFromModel(clf, prefit=True)
X_new = model.transform(X)
X_new.shape

(150, 2)

特征监控

在数据分析和挖掘中，特征占据着很重要的地位。因此，我们需要对重要的特征进行监控与有效性分析，了解模型所用的特征是否存在问题，当某个特别重要的特征出现问题时，需要做好备案，防止灾难性结果。

• 数据缺失
• 数据异常
• ……

感谢倾听

本作品采用 授权

版权所有 © 范叶亮 Leo Van