K-means
K-means 是一种简单的迭代性的聚类算法。对于数据集 \(D = \{x_1, x_2, ..., x_n\}\)，其中 \(x_i \in \mathbb{R}^d\)，需要指定利用 K-means 算法对数据划分成 \(k\) 个簇。对于数据集 \(D\) 的每个点 \(x_i\) 仅属于一个簇 \(S_i\)，则 K-means 算法的目标函数可以表示为：
\[
\underset{S}{\operatorname{argmin}} \sum_{i=1}^{k} \sum_{x \in S_i} \|x - \mu_i\|_2^2
\]
其中 \(\mu_i\) 是簇 \(S_i\) 的均值向量。从目标函数不难看出，K-means 是通过一种“紧密程度”的形式对数据进行划分的，衡量这种“紧密程度”一般我们会用到“距离”的概念。距离可以理解为在集合 \(M\) 上的一个度量（Metric），即
\[
dist: M \times M \to \mathbb{R}
\]
K-means
对于集合 \(M\) 中的 \(x, y, z\)，下列条件均成立：
- \(dist\left(x, y\right) \geq 0\)（非负性）
- \(dist\left(x, y\right) = 0\) 当且仅当 \(x = y\)（同一性）
- \(dist\left(x, y\right) = dist\left(y, x\right)\)（对称性）
- \(dist\left(x, z\right) \leq dist\left(x, y\right) + dist\left(y, z\right)\)（三角不等式）
对于点 \(x = \left(x_1, x_2, ..., x_n\right)\) 和点 \(y = \left(y_1, y_2, ..., y_n\right)\)，常用的距离为 \(p\) 阶明可夫斯基距离（Minkowski distance）：
\[
dist\left(x, y\right) = \left(\sum_{i=1}^{n} |x_i - y_i|^p\right)^{\frac{1}{p}}
\]
K-means
当 \(p = 1\) 时，称之为曼哈顿距离（Manhattan distance）或出租车距离：
\[
dist_{man}\left(x, y\right) = \sum_{i=1}^{n} |x_i - y_i|
\]
当 \(p = 2\) 时，称之为欧式距离（Euclidean distance）：
\[
dist_{ed}\left(x, y\right) = \sqrt{\sum_{i=1}^{n} \left(x_i - y_i\right)^2}
\]
曼哈顿距离和欧式距离直观比较如图所示：
K-means
对于 K-means 算法，具体的计算过程如下：
- 指定簇的个数为 \(k\)，并随机设置 \(k\) 个簇的中心，对于簇 \(S_i\) 其中心为 \(\mu_i\)。
- 计算数据集 \(D = \{x_1, x_2, ..., x_n\}\) 中的所有点 \(x_j\) 到每个簇的中心 \(\mu_i\) 的距离 \(dist\left(x_j, \mu_i\right)\)。
- 对于点 \(x_j\)，从其到每个簇中心 \(\mu_i\) 的距离中选择距离最短的簇作为本轮计算中该点所隶属的簇。
- 对于隶属于同一个簇的样本 \(D_{S_i}\)，计算这些样本点的中心，作为该簇新中心 \(\mu'_i\)。
- 重复执行步骤 2 到步骤 4 直至簇中心不再发生变化或超过最大迭代次数。
通过上述步骤的计算，K-means 算法可以将样本点划分为 \(k\) 个簇，并得到每个簇的最终中心 \(\mu_i\)。
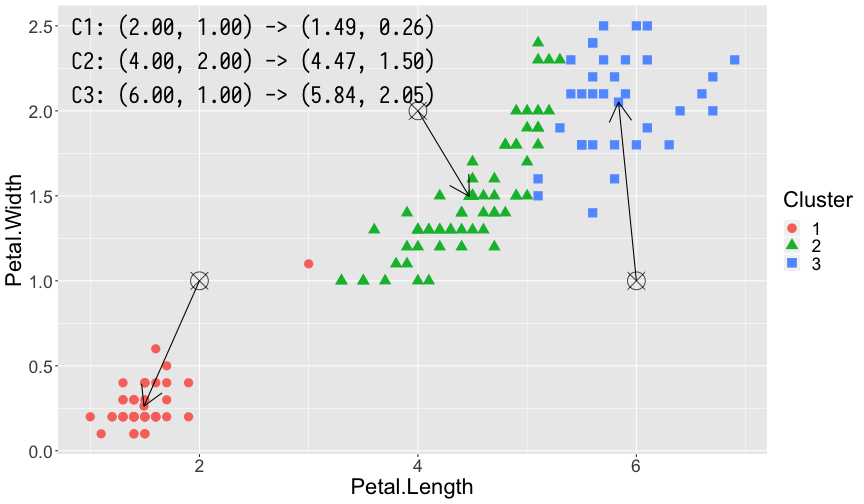
利用 K-means 算法，我们对 iris 数据集进行聚类分析。iris 数据集包含了 Sepal.Length，Sepal.Width，Petal.Length，Petal.Width 以及花的种类共 5 列数据。为了能够更直观的演示，我们仅采用 Petal.Length 和 Petal.Width 两列数据。K-means 是一种无监督的学习算法，因此我们并没有先验知识知道数据最适合分为几个簇，同时 K-means 算法又是一个对于聚类中心初始点敏感的算法，因此同样为了便于演示效果，在此我们设置簇的个数 \(k = 3\)，\(3\) 个簇对应的初始中心点分别为 \(\mu_1 = \left(2, 1\right), \mu_2 = \left(4, 2\right), \mu_3 = \left(6, 1\right)\)。
K-means
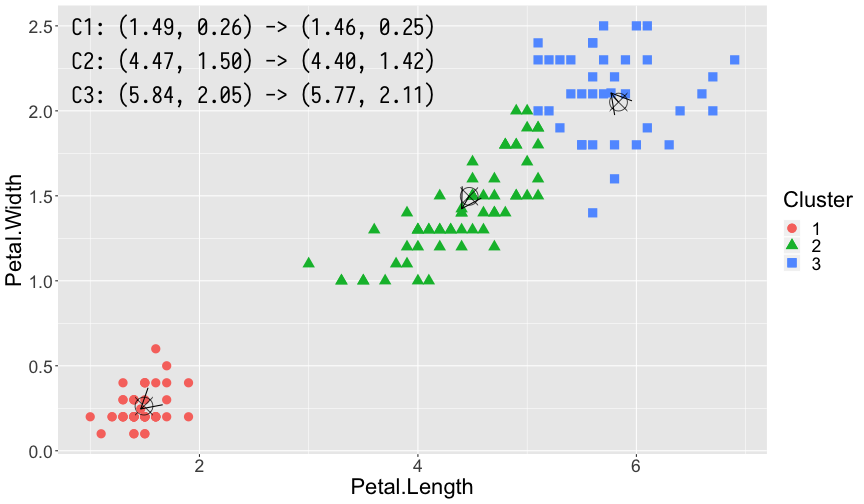
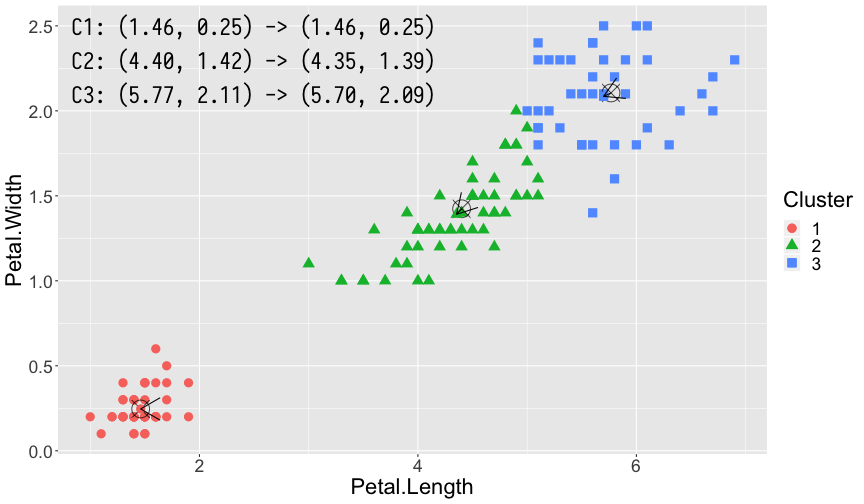
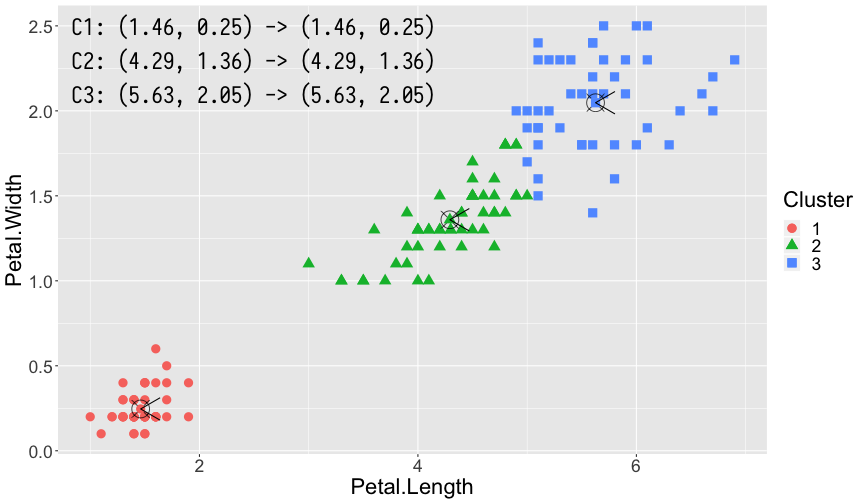
第 1 轮，第 2 轮，第 3 轮和第 7 轮（最终轮）计算得出的结果。其中每幅图左上角 3 组坐标分别表示了 3 个簇的中心更新前和更新后的位置。图中的 ⦻ 号即为更新前簇的中心，箭头指向的方向即为更新后簇的中心，每轮计算中隶属不同簇的样本点利用颜色和形状加以了区分。
K-means 算法在一般数据集上可以的到较好的聚类效果，但同时也存在若干问题：
- K-means 算法需要预先设置聚类个数 \(k\)。
- K-means 是一个对于簇中心点起始位置敏感的算法，设置不同的簇中心点的起始位置可能得到不同的聚类结果。
- 噪音数据对 K-means 算法的聚类结果影响较大。
- 只能发现球状簇。
K-means
sklearn.cluster.KMeans(
n_clusters=8, *, init='k-means++', n_init='auto', max_iter=300, tol=0.0001, verbose=0, random_state=None,
copy_x=True, algorithm='lloyd')
常用的参数如下表所示：
n_clusters |
聚类个数 |
init |
初始化方法，'k-means++', 'random' 或指定位置 |
n_init |
利用 centroid seeds 运行算法的次数 |
max_iter |
最大迭代次数 |
algorithm |
K-means 使用的算法，'full', 'elkan' |
K-means
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
y_pred = KMeans(n_clusters=3).fit_predict(X[:, 2:])
plot_df = pd.DataFrame(
{'x': X[:, 2], 'y': X[:, 3], 'h': y_pred})
sns.scatterplot(
data=plot_df, x='x', y='y', s=100, hue='h',
palette=sns.color_palette('husl', 3))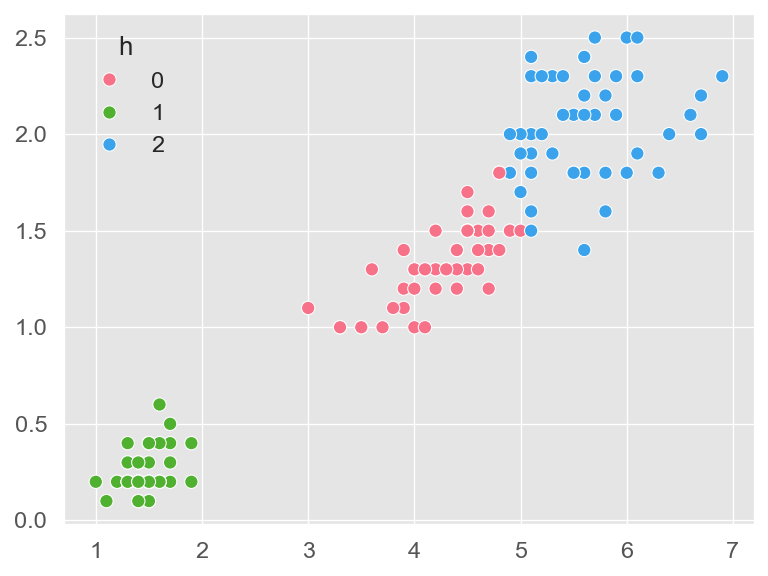
层次聚类
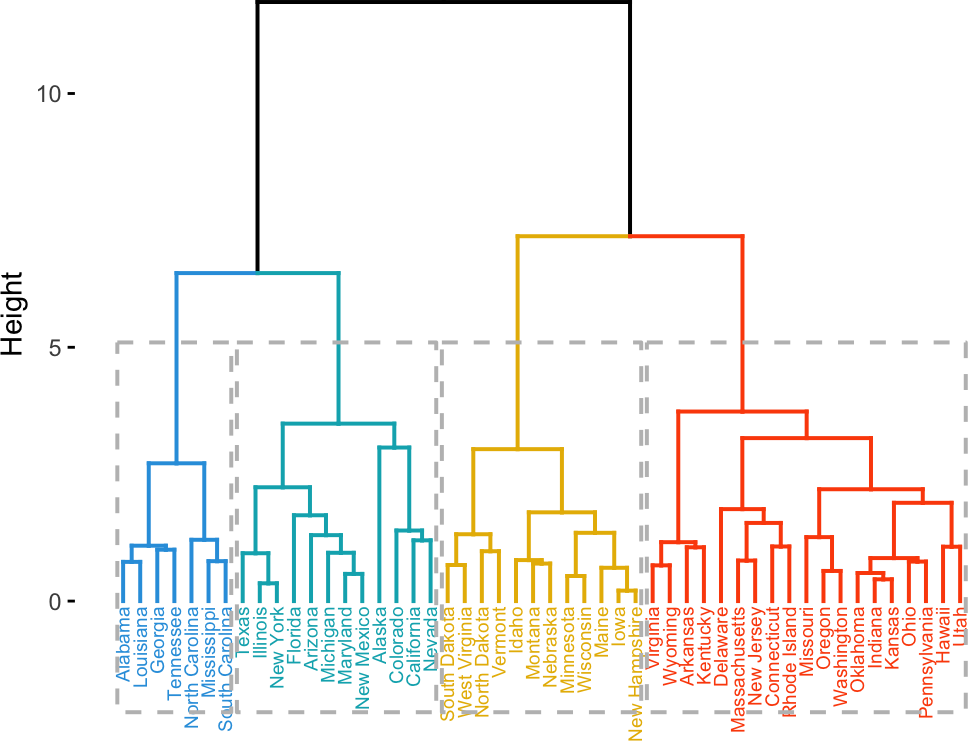
层次聚类（hierarchical clustering）不同于 K-means 那种基于划分的聚类，通过对数据集在不同层次上进行划分，直至达到某种条件。层次聚类根据分层的方法不同，可以分为凝聚（agglomerative）层次聚类和分裂（divisive）层次聚类。
AGNES（Agglomerative Nesting）算法是一种凝聚层次聚类算法，其基本思想如下：
- 将数据集中每个样本作为一个簇。
- 在每一轮计算中，找出两个距离最近的簇进行合并，生成一个新的簇。
- 重复步骤 2，直至达到预设的聚类簇的个数。
层次聚类
因此，对于 AGNES 算法而言，最关键的是如何计算两个簇之间的距离，对于簇 \(C_i\) 和簇 \(C_j\)，常用的距离计算方法有：
\[
dist_{min} = \min \{dist\left(x, y\right) | x \in C_i, y \in C_j\}
\]
\[
dist_{max} = \max \{dist\left(x, y\right) | x \in C_i, y \in C_j\}
\]
\[
dist_{avg} = \dfrac{1}{|C_i| |C_j|} \sum_{x \in C_i} \sum_{y \in C_j} dist\left(x, y\right)
\]
\[
dist_{med} = dist\left(Median_{C_i}, Median_{C_j}\right)
\]
层次聚类
DIANA（Divisive Analysis）算法是一种分裂层次聚类算法，其基本思想如下：
- 将数据集中全部样本作为一个簇。
- 在每一轮计算中，对于“最大”的簇 \(C\)，找到 \(C\) 中与其他点的平均相异度最大的点 \(p_0\)，将其放在一个新的簇 \(C_{new}\) 中，剩余的点此时所组成的簇为 \(C_{old}\)。
- 在簇 \(C_{old}\) 找到一个距离簇 \(C_{new}\) 最近，且距离小于到簇 \(C_{old}\) 的点 \(p_i\)，并将其加入到簇 \(C_{new}\) 中。
- 重复步骤 3，直至无法找到符合条件的点 \(p_i\)，此时得到两个新簇 \(C_{old}\) 和 \(C_{new}\)。
- 重复步骤 2 和步骤 3，直至达到预设的聚类簇的个数。
在 DIANA 算法中，衡量一个簇 \(C\) 的大小，一般利用簇的直径，即簇中任意两个样本之间距离的最大值；衡量簇 \(C\) 中一个点 \(p\) 的平均相异度，一般利用该点到簇中其他点距离的平均值。
层次聚类
sklearn.cluster.AgglomerativeClustering(
n_clusters=2, *, metric='euclidean', memory=None, connectivity=None, compute_full_tree='auto', linkage='ward',
distance_threshold=None, compute_distances=False)
n_clusters |
聚类个数 |
affinity |
计算连接使用的度量，'euclidean', 'l1', 'l2', 'manhattan', 'cosine', 'precomputed' |
connectivity |
连接矩阵 |
compute_full_tree |
是否计算完整树 |
linkage |
连接准则，'ward', 'complete', 'average', 'single' |
distance_threshold |
距离阈值，大于该阈值则不合并 |
层次聚类
import numpy as np
from sklearn.cluster import AgglomerativeClustering
X = np.array([
[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
clustering = AgglomerativeClustering().fit(X)
clustering
AgglomerativeClustering()
array([1, 1, 1, 0, 0, 0])
clustering.n_connected_components_
授权