import statsmodels.api as sm
import matplotlib.pyplot as plt
from scipy import stats
from statsmodels.graphics.tsaplots import plot_predict
from statsmodels.graphics.api import qqplot
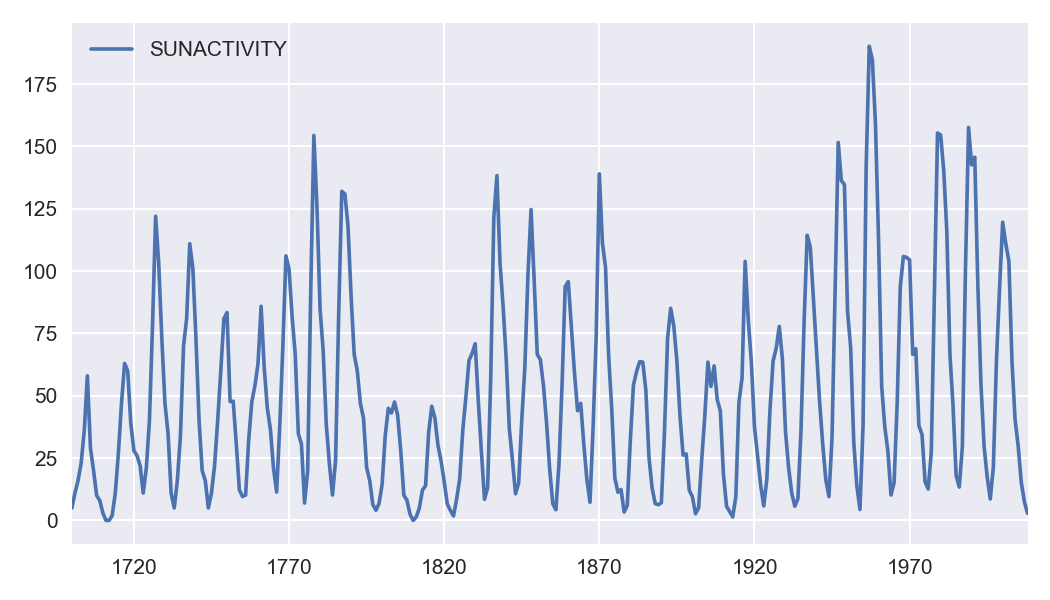
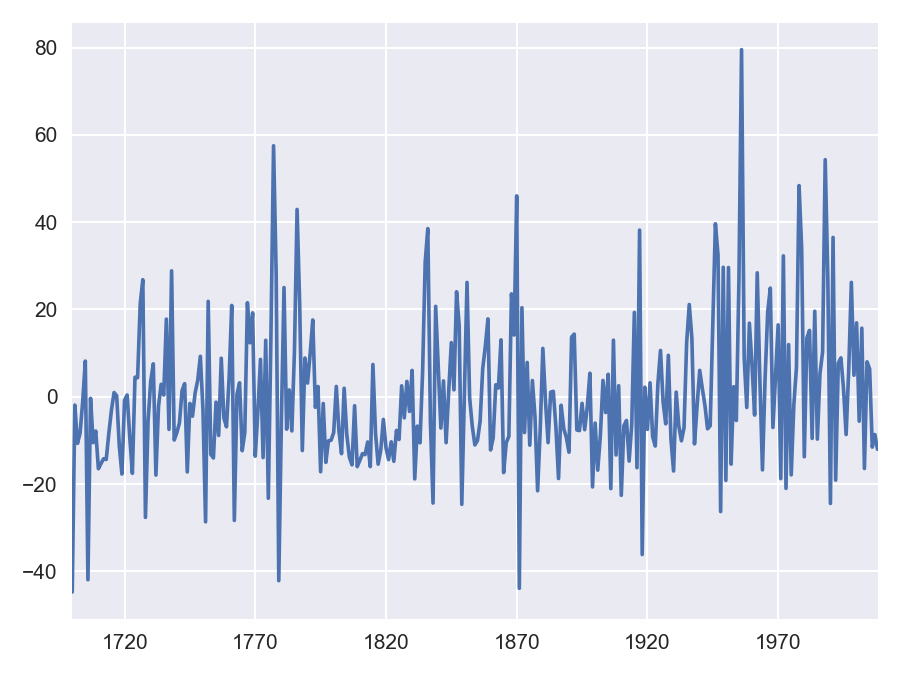
dta = sm.datasets.sunspots.load_pandas().data
sm.datasets.sunspots.NOTE时间序列算法
Time Series Algorithms
目录
- 时间序列
- ARIMA 模型
- 季节性分析
- Prophet
时间序列
时间序列
时间序列是现实生活中经常会碰到的数据形式。例如北京市连续一年的日平均气温、某股票的股票价格、电商平台上某件商品的日销售件数等等。时间序列分析的目的是挖掘时间序列中隐含的信息与模式,并借此对此序列数据进行评估以及对序列的后续走势进行预测。

时间序列
假设存在一个时间序列:\(\left\{Y_t | t = 0, \pm 1, \pm 2, ...\right\}\)
均值定义为:\(\mu_t = E\left(Y_t\right)\)
方差定义为:\(\sigma_{t}^{2} = E \left(\left(Y_t - \mu_t\right)^2\right)\)
自协方差定义为:\(\gamma_{t, s} = Cov\left(Y_t, Y_s\right) = E\left(\left(Y_t - \mu_t\right) \left(Y_s - \mu_s\right)\right)\)
自相关系数定义为:\(\rho_{t, s} = \dfrac{\gamma_{t, s}}{\sqrt{\gamma_{t, t} \gamma_{s, s}}}\)
如果忽略元素来自时间序列这一事实,各统计量的意义与普通的统计学中无异。
白噪声
考虑一个时间序列,其中每一个元素为独立同分布变量,且均值为 0。这种时间序列叫做白噪声。之所以叫这个名字,是因为对这种序列的频域分析表明其中平等的包含了各个频率,和物理中的白光类似。
每个元素服从 \(N\left(0, 1\right)\),均值 \(\mu_t = 0\),方差 \(\sigma_t^2 = 1\)。每个元素独立,对于任何 \(t \neq s\),\(\gamma_{t, s} = 0\),\(\rho_{t, s} = 0\)。
我们一般用 \(e\) 表示白噪声,将白噪声序列写作:
\[ \left\{e_1, e_2, ..., e_t, ...\right\} \]
白噪声
考虑一个时间序列,在 \(t\) 时刻的值是白噪声前 \(t\) 个值之和,设 \(\left\{e_1, e_2, ..., e_t, ...\right\}\) 为标准正态的白噪声,则:
\[ \begin{split} Y_1 &= e_1 \\ Y_2 &= e_1 + e_2 \\ &\vdots \\ Y_t &= e_1 + e_2 + ... + e_t \\ &\vdots \end{split} \]
\(\mu_t = E\left(e_1 + ... + e_t\right) = E\left(e_1\right) + ... + E\left(e_t\right) = 0\)
\(\sigma_t^2 = Var\left(e_1 + ... + e_t\right) = Var\left(e_1\right) + ... + Var\left(e_t\right) = t \sigma^2\)
统计上可以看出随机游走的“趋势性”实际是个假象,因为其均值一直是白噪声的均值,不存在偏离的期望。但方差与时间呈线性增长并且趋向于无穷大,这意味着只要时间够长,随机游走的序列值可以偏离均值任意远,但期望永远在均值处。物理与经济学中很多现象被看做是随机游走,例如分子布朗运动,股票价格走势等。
平稳性
平稳性是时间序列分析中很重要的一个概念。一般的,认为一个时间序列是平稳的,如果它同时满足一下两个条件:
- 均值函数是一个常数函数
- 自协方差函数只与时滞有关,与时间点无关
一般的时间序列分析往往针对平稳序列,对于非平稳序列会通过某些变换将其变为平稳的。
ARIMA 模型
ARIMA 模型
ARIMA 模型(Autoregressive Integrated Moving Average model),差分整合移动平均自回归模型,又称整合移动平均自回归模型(移动也可称作滑动),是时间序列预测分析方法之一。
\(\text{ARIMA} \left(p, d, q\right)\) 中,\(\text{AR}\) 是自回归,\(p\) 为自回归项数;\(\text{MA}\) 为滑动平均,\(q\) 为滑动平均项数,\(d\) 为使之成为平稳序列所做的差分次数(阶数)。
AR 模型
具有如下结构的模型为 \(p\) 阶自回归模型,记为 \(AR\left(p\right)\):
\[ Y_t = e_t + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + ... + \phi_p Y_{t-p} \]
\(AR\left(p\right)\) 模型有三个限制条件:
- \(\phi_p \neq 0\),这个限制条件可以保证模型的最高阶数为 \(p\);
- \(e_t \sim N \left(0, \sigma_t^2\right)\),这个限制条件要求随机干扰序列 \(e_t\) 是均值为零的白噪声序列。
- \(E\left(Y_s e_t\right) = 0, \forall s < t\),这个条件限制当前的随机干扰与过去的数据序列值无关。
通常上述三个条件为 AR 模型的默认条件,因此常将 \(AR\left(p\right)\) 模型简记为:
\[ Y_t = \sum_{i=1}^{p}{\phi_i Y_{t-i}} + e_t \]
MA 模型
具有如下结构的模型为 \(q\) 阶滑动平均模型,记为 \(MA\left(q\right)\):
\[ Y_t = e_t - \theta_1 e_{t-1} - \theta_2 e_{t-2} - ... - \theta_q e_{t-q} \]
\(MA\left(q\right)\) 模型有两个限制条件:
- \(\theta_q \neq 0\),这个限制条件可以保证模型的最高阶数为 \(q\);
- \(e_t \sim N \left(0, \sigma_t^2\right)\),这个限制条件要求随机干扰序列 \(e_t\) 是均值为零白噪声序列。
通常上述两个条件为MA模型的默认条件,因此常将 \(MA\left(q\right)\) 模型简记为:
\[ Y_t = e_t - \sum_{i=1}^{q}{\theta_i e_{t-i}} \]
ARMA 模型
如果一个时间序列兼有 AR 和 MA 部分,并且是平稳的,则构成 ARMA 模型。一般 \(ARMA\left(p, q\right)\) 的表达式为:
\[ Y_t = e_t + \sum_{i=1}^{p}{\phi_i Y_{t-i}} - \sum_{j=1}^{q}{\theta_j e_{t-j}} \]
令:
\[ \Phi\left(L\right) = 1 - \phi_1 L - \phi_2 L^2 - ... - \phi_p L^p \]
\[ \Theta\left(L\right) = 1 + \theta_1 L + \theta_2 L^2 + ... + \theta_q L^q \]
则上式可简写为:
\[ \Phi\left(L\right)Y_t = \delta + \Theta\left(L\right) e_t \]
其中,\(L\) 称之为滞后算子。
ARIMA 模型
ARIMA 和 ARMA 的区别就是,将公式中 \(Y_t\) 替换为差分算子,即:
\[ \Phi\left(L\right) \Delta^d Y_t = \delta + \Theta\left(L\right) e_t \]
差分算子为:
\[ \begin{split} \Delta Y_t &= Y_t - Y_{t-1} = Y_t - L Y_t = \left(1 - L\right) Y_t \\ \Delta^2 Y_t &= \Delta Y_t - \Delta Y_{t-1} = \left(1 - L\right) Y_t - \left(1 - L\right) Y_{t-1} = \left(1 - L\right)^2 Y_t \\ \Delta^d Y_t &= \left(1 - L\right)^d Y_t \end{split} \]
参数优化:
- 确定差分阶数 \(d\),从而保证差分后的时间序列是平稳的。
- 确定 AR 和 MA 模型的参数 \(p\) 和 \(q\),例如 AIC 等。
ARIMA 模型
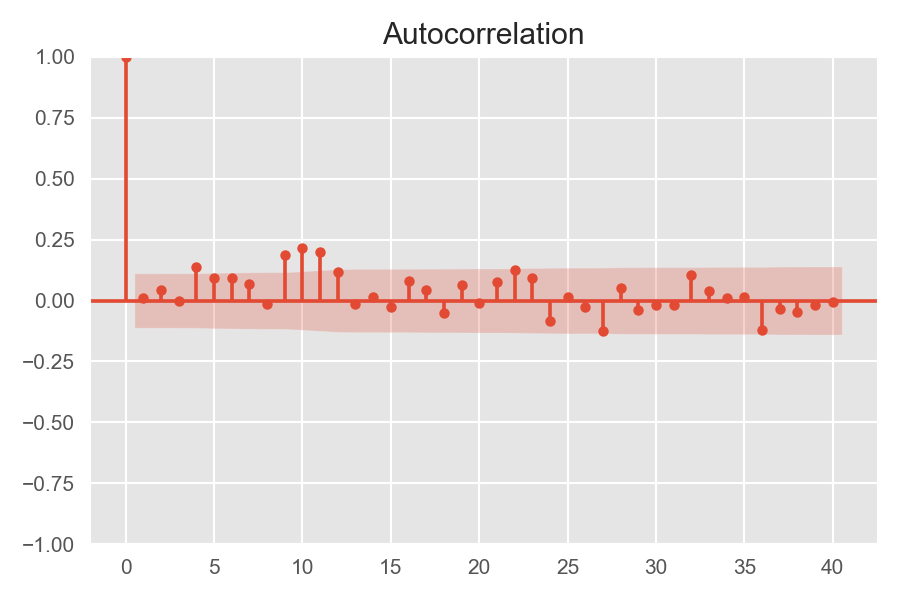
自相关函数(ACF):延迟为 \(k\) 时,这是相距 \(k\) 个时间间隔的序列值之间的相关性。
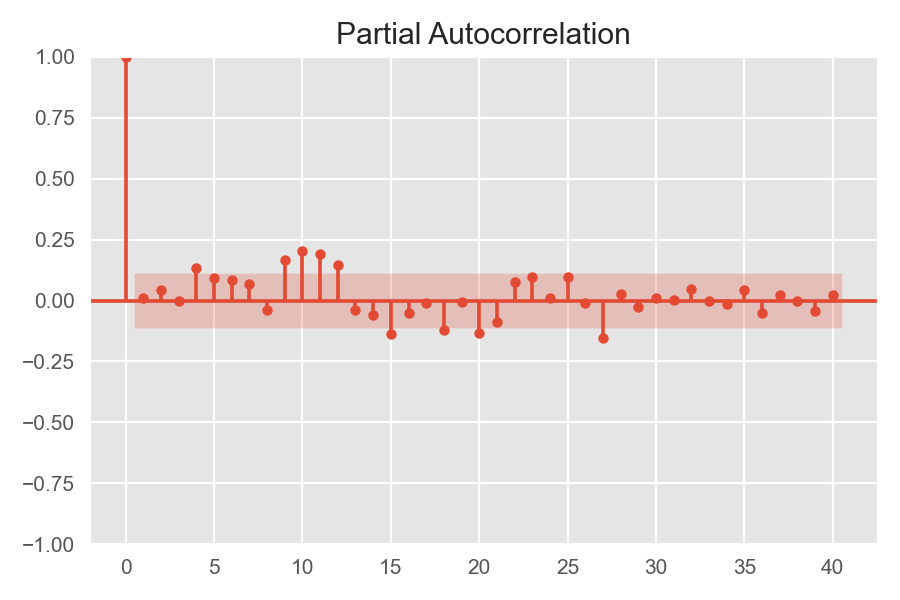
偏自相关函数(PACF)。延迟为 \(k\) 时,这是相距 \(k\) 个时间间隔的序列值之间的相关性,同时剔除了中间 \(k-1\) 个随机变量的干扰。
拖尾即始终有非零取值,不会在 \(k\) 大于某个常数后就恒等于零(或在 0 附近随机波动)。 截尾即在大于某个常数 \(k\) 后快速趋于 0。
- AR 模型:自相关系数拖尾,偏相关系数截尾
- MA 模型:自相关系数截尾,偏相关系数拖尾
- ARMA 模型:自相关系数和偏相关系数均拖尾
利用 ACF 和 PACF 图的拖尾和截尾性质判断 ARMA 模型的方法如下表所示:
| 模型 | ACF | PACF |
|---|---|---|
| 白噪音 | 全部为零 | 全部为零 |
| \(AR \left(p\right)\) | 拖尾 | \(p\) 阶后截尾 |
| \(MA \left(q\right)\) | \(q\) 阶后截尾 | 拖尾 |
| \(ARMA \left(p, q\right)\) | \(q\) 阶后拖尾 | \(p\) 阶后拖尾 |
ARIMA 模型
Number of Observations - 309 (Annual 1700 - 2008)
Number of Variables - 1
Variable name definitions::
SUNACTIVITY - Number of sunspots for each year
The data file contains a 'YEAR' variable that is not returned by load.ARMA 模型
ARMA 模型
const 49.746198
ar.L1 1.390633
ar.L2 -0.688573
sigma2 274.727182
dtype: float64(2622.637093301597, 2637.5704584091877, 2628.607481146843)(2619.40362924567, 2638.0703356301588, 2626.8666140522273)ARMA 模型
ARMA 模型
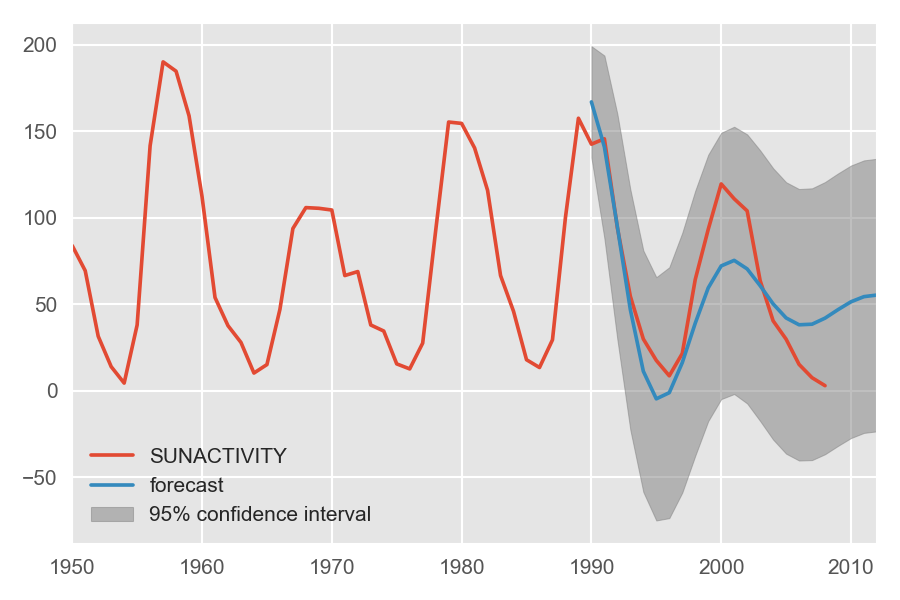
ARMA 模型
1990-12-31 167.048337
1991-12-31 140.995022
1992-12-31 94.862115
1993-12-31 46.864439
1994-12-31 11.246106
1995-12-31 -4.718265
Freq: YE-DEC, Name: predicted_mean, dtype: float64季节性分析
季节性分析
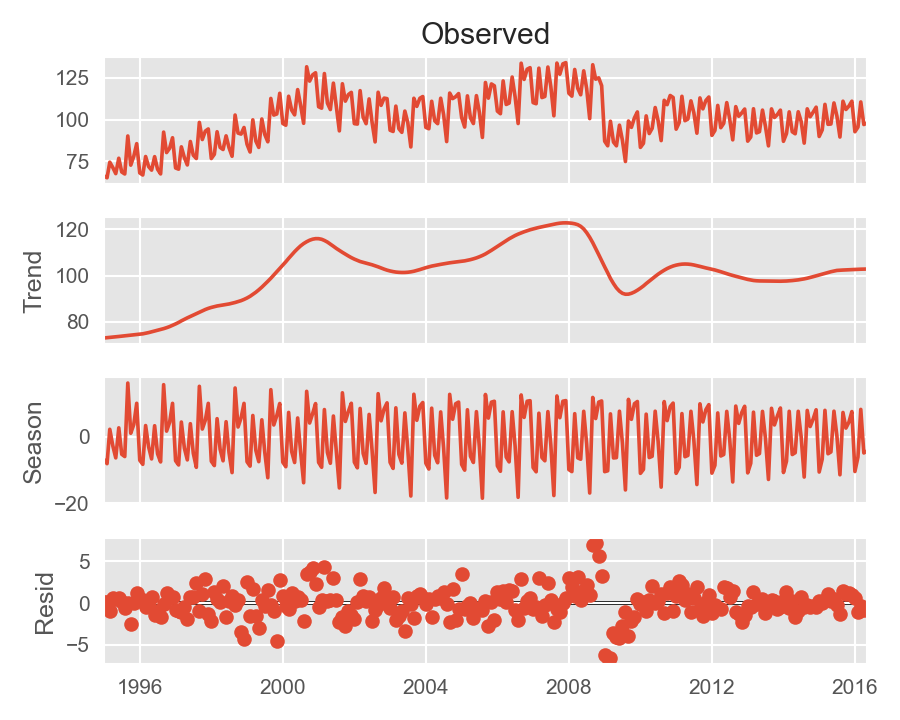
STL (Seasonal-Trend decomposition procedure based on Loess) 1 为时序分解中一种常见的算法,基于局部回归(Loess)将某时刻的数据 \(Y_v\) 分解为趋势分量(trend component)、周期分量(seasonal component)和余项(remainder component):
\[ Y_v = T_v + S_v + R_v \quad v = 1, ..., N \]
季节性分析
STS.M.I7.W.TOVT.NS0016.4.000
count 257.000000
mean 100.574591
std 15.698298
min 65.150000
25% 90.260000
50% 100.990000
75% 111.550000
max 134.140000Prophet
Prophet
Prophet 1 2 是一个基于加法模型的时间序列预测算法,其中非线性趋势通过年,周,日的季节性和节假日效应进行拟合。它最适合具有强烈季节性影响和多个季节历史数据的时间序列。Prophet 对数据缺失和趋势变化具有鲁棒性,通常可以很好地处理异常值。
- 准确且快速:Prophet 在 Facebook 的许多应用中用于对计划和目标设定进行可靠的预测。在大多数情况下,我们发现它的效果要比其他任何方法都要好。Prophet 利用 Stan 拟合模型,可以在几秒钟内获得预测结果。
- 全自动:无需人工干预即可获得杂乱数据的合理预测。Prophet 对异常值,数据缺失以及时间序列中的急剧变化具有鲁棒性。
- 可调整的预测:Prophet 为用户提供了许多可调整项,可以通过领域知识设置易于理解的参数从而改善预测效果。
- 可在 R 或 Python 中使用:在 R 和 Python 中均实现了 Prophet,其共享相同的基础 Stan 代码。
Prophet 入门
Prophet 使用 sklearn 的 API,在创建 Prophet 实例后可以调用其 fit 和 predict 方法。
Prophet 的输入为包含两列数据(ds 和 y)的数据框。其中 ds(datestamp)为 pandas 可接受的数据格式,理想情况下日期格式为 YYYY-MM-DD,日期时间格式为 YYYY-MM-DD HH:MM:SS。y 列必须为数值类型,表示我们所需要预测的值。
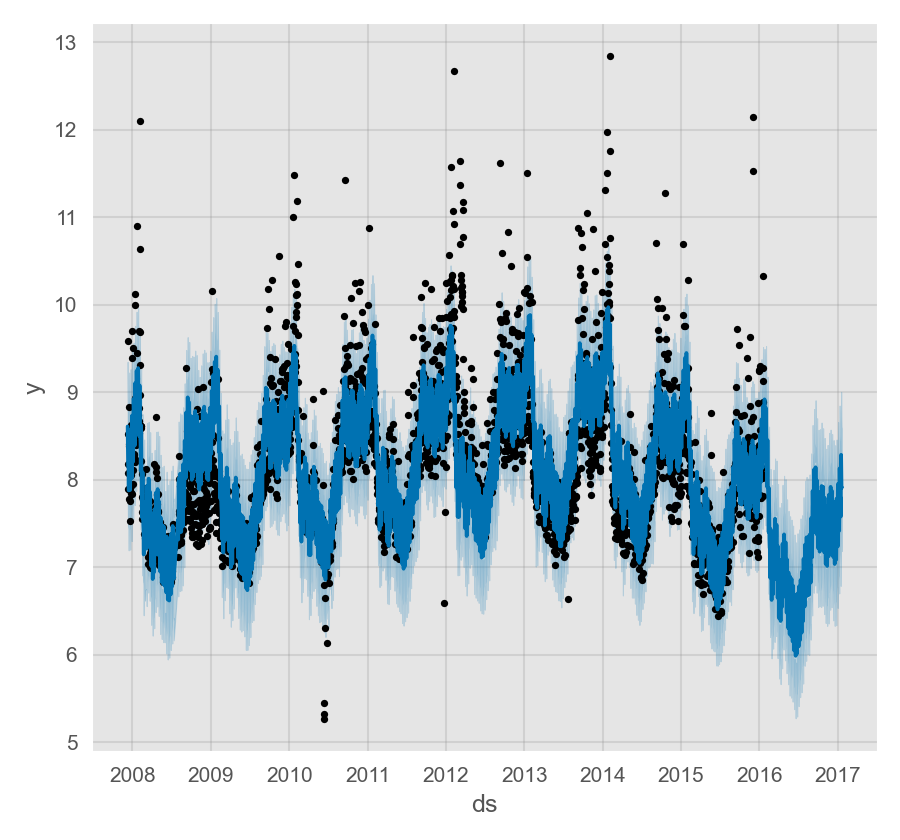
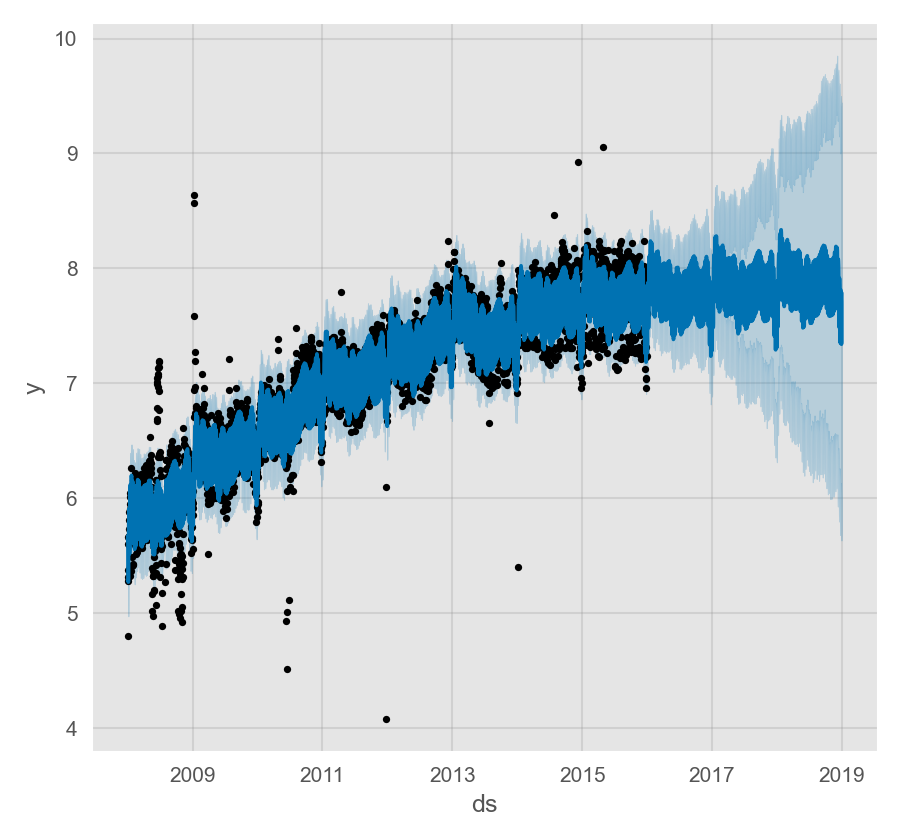
我们以 Wikipedia 中 Peyton Manning 页面浏览量 1 的时间序列为例来说明 Prophet 的相关功能。
Prophet 入门
通过实例化 Prophet 对象构建模型,所有参数在实例化时传入。调用 fit 方法并传入历史数据进行拟合:
Prophet 入门
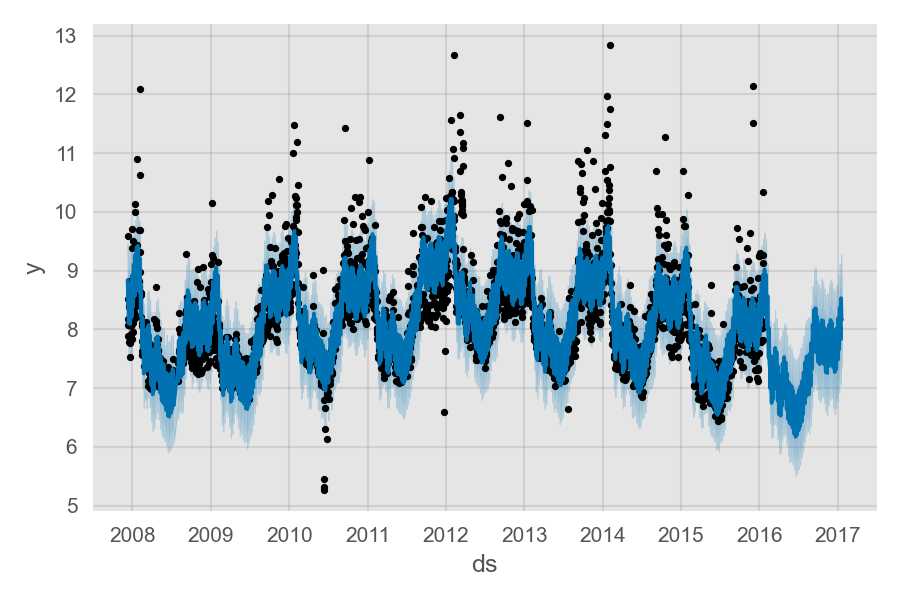
predict 方法会将预测值保存在数据框的 yhat 列内。
ds yhat yhat_lower yhat_upper
3265 2017-01-15 8.208400 7.460680 8.920662
3266 2017-01-16 8.533418 7.791344 9.275319
3267 2017-01-17 8.320838 7.572588 9.098316
3268 2017-01-18 8.153458 7.457548 8.898186
3269 2017-01-19 8.165398 7.367720 8.932801Prophet 入门
Prophet 预测增长
默认情况下 Prophet 利用线性模型进行预测。在预测增长时,通常会设置一个最大可达到的点,例如:市场总规模,人口总数等。我们称其为承载能力,也就是预测在这个点达到饱和。
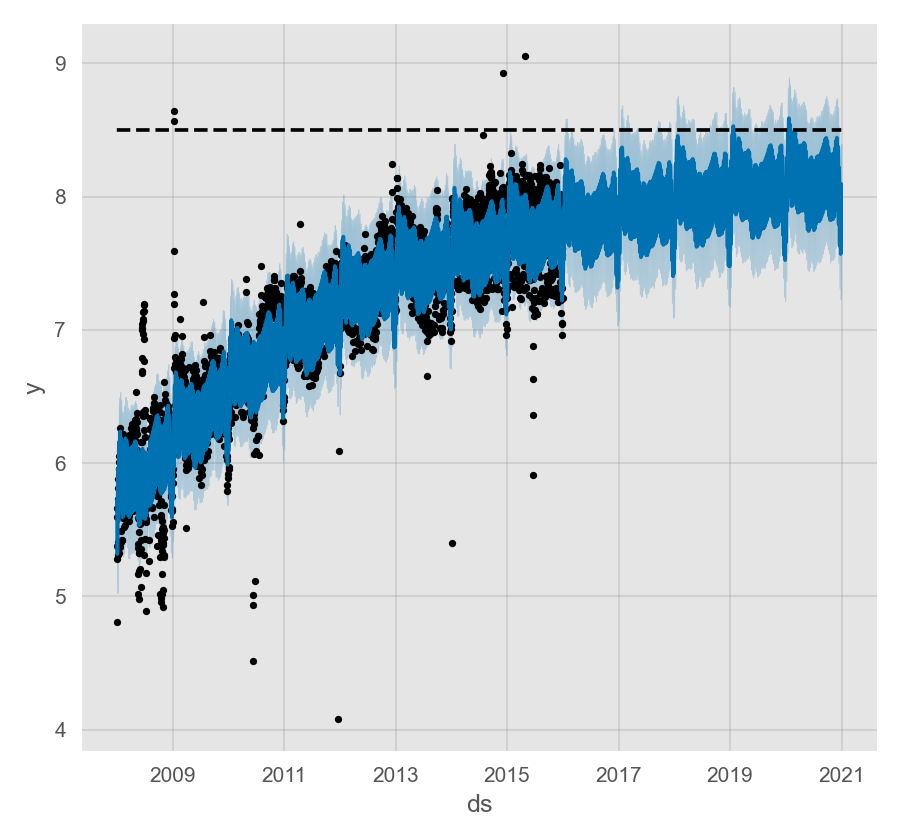
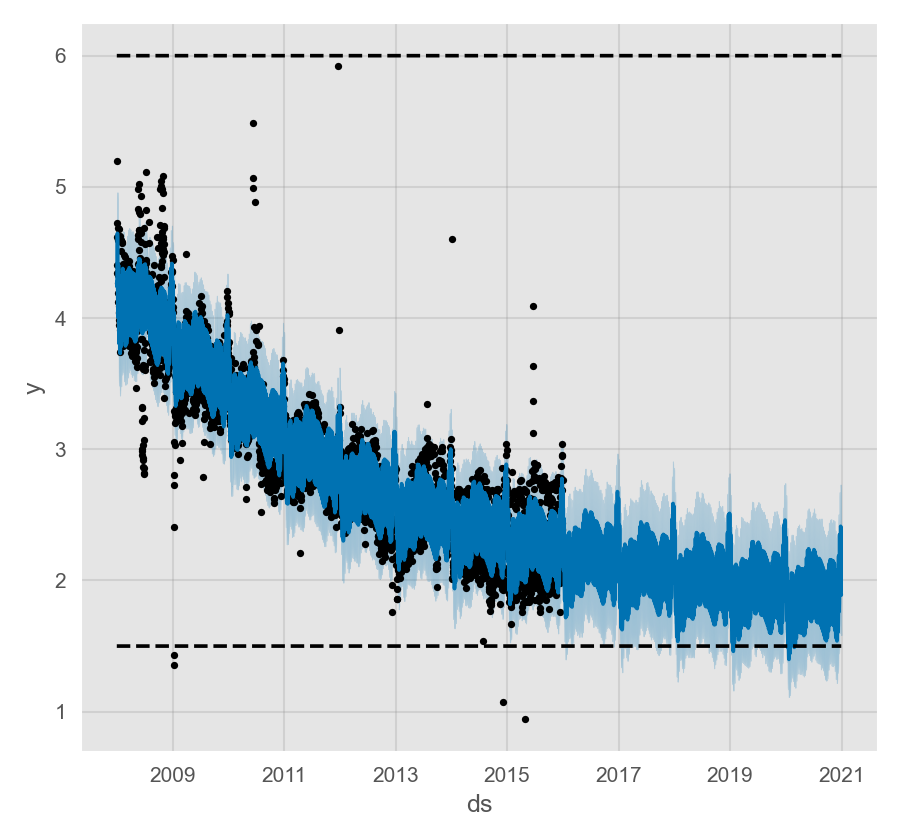
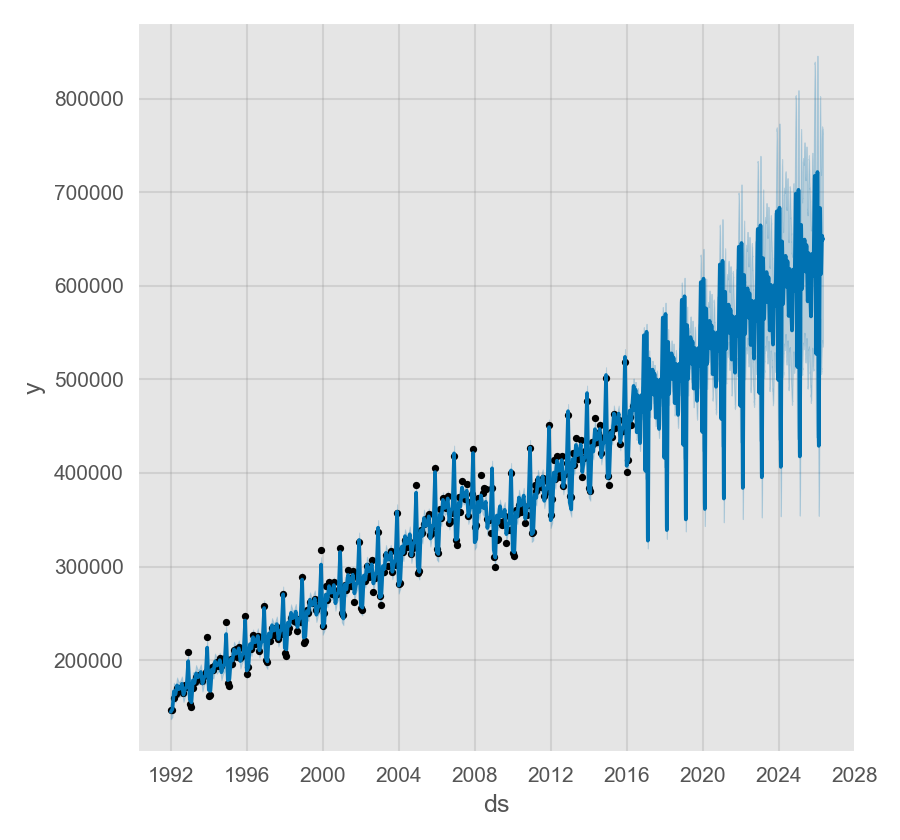
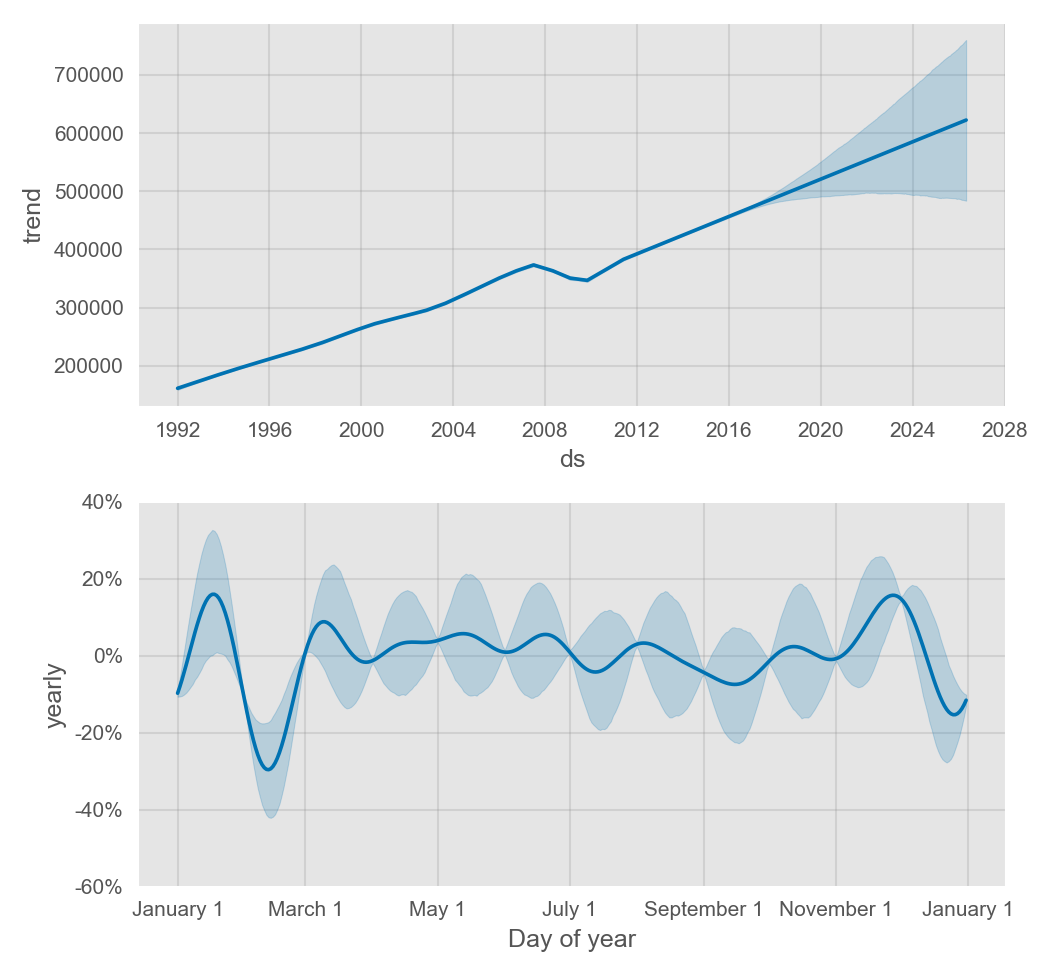
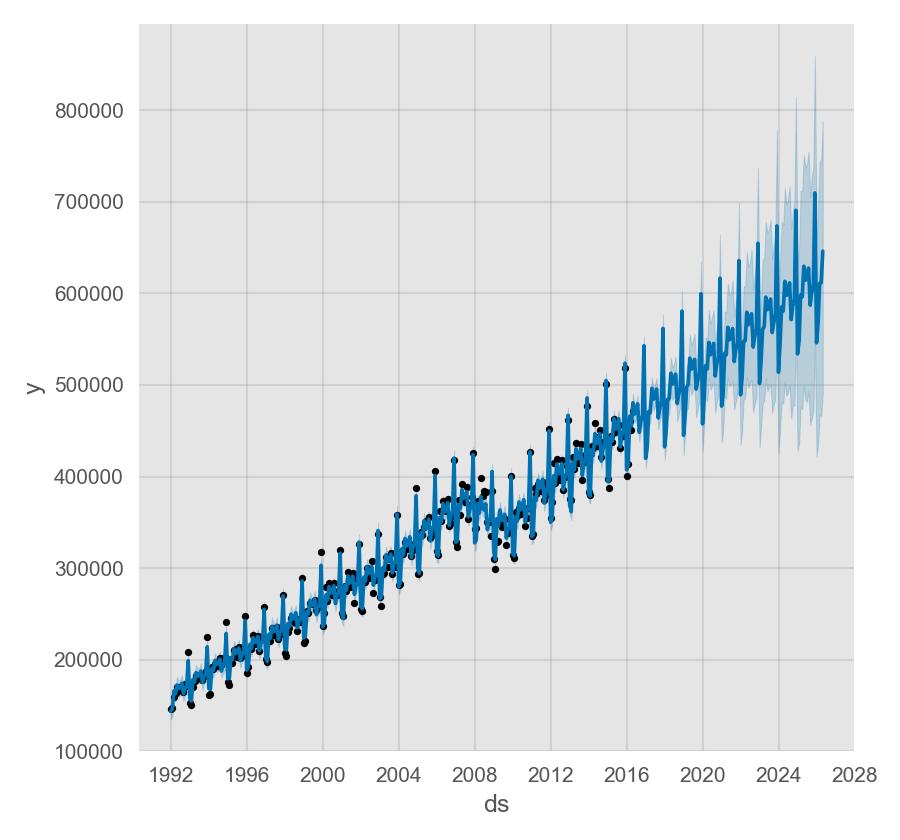
Prophet 使用可指定承载能力的 Logistic Growth Trend 模型进行预测,以 Wikipedia 上 R (programming language) 页面的访问日志为例:
通过 cap 列指定承载能力:
Prophet 预测增长
Prophet 预测增长
Prophet 趋势突变点
从之前的示例中可以发现,实时的时间序列在其轨迹中经常会有突变。默认情况下,Prophet 会自动检测这些突变点,并对趋势做适当调整。如果在对趋势建模时发生了一些问题,例如:Prophet 不小心忽略了一个趋势速率的变化或者对历史数据趋势变化存在过拟合现象,希望对趋势的调整过程做更好地控制的话,可以使用下面介绍几种的方法。
Prophet 首先通过在大量潜在的突变点(变化速率突变)中进行识别来监测突变点。之后对趋势变化的幅度做稀疏化(等同于 L1 正则化),实际上 Prophet 在建模时会存在很多变化速率突变的点,但只会尽可能少地使用它们。
Prophet 趋势突变点
以之前的 Peyton Manning 页面的浏览量数据为例,默认情况下,Prophet 会识别出 25 个潜在的突变点(均匀分布在在前 80% 的时间序列数据中)。下图中的竖线指出这些潜在的突变点所在的位置:
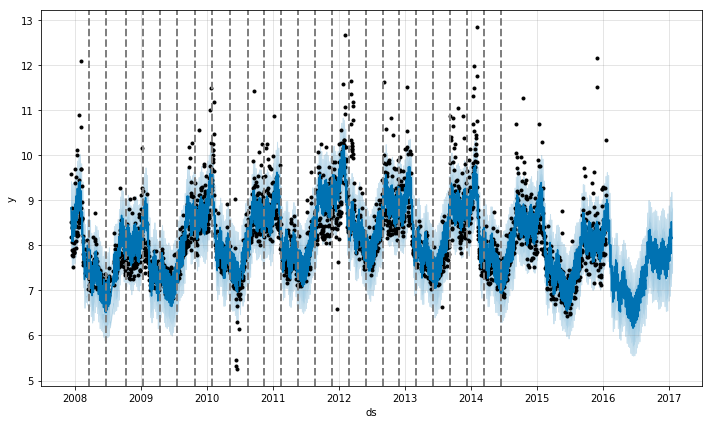
虽然存在很多变化速率可能会突变的点,但由于做了稀疏先验,绝大多数突变点并不会包含在建模过程中。如下图示,通过观察对每个突变点绘制的速率变化值图,可以发现这一点:
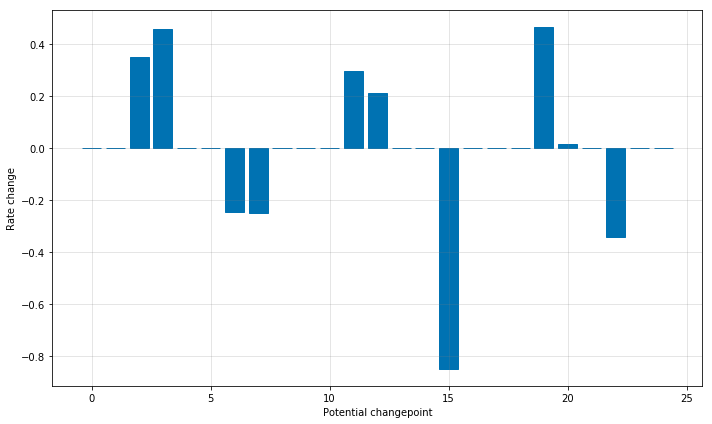
Prophet 趋势突变点
潜在突变点的数量可以通过设置 n_changepoints 参数来指定,但最好还是利用调整正则化过程来自动修正。
默认情况下,仅在时间序列的前 80% 推断突变点,以便有足够的空间来预测趋势并避免在时间序列末尾过拟合。默认值在大多数情况下是适用的,通过 changepoint_range 可以对其进行设置。
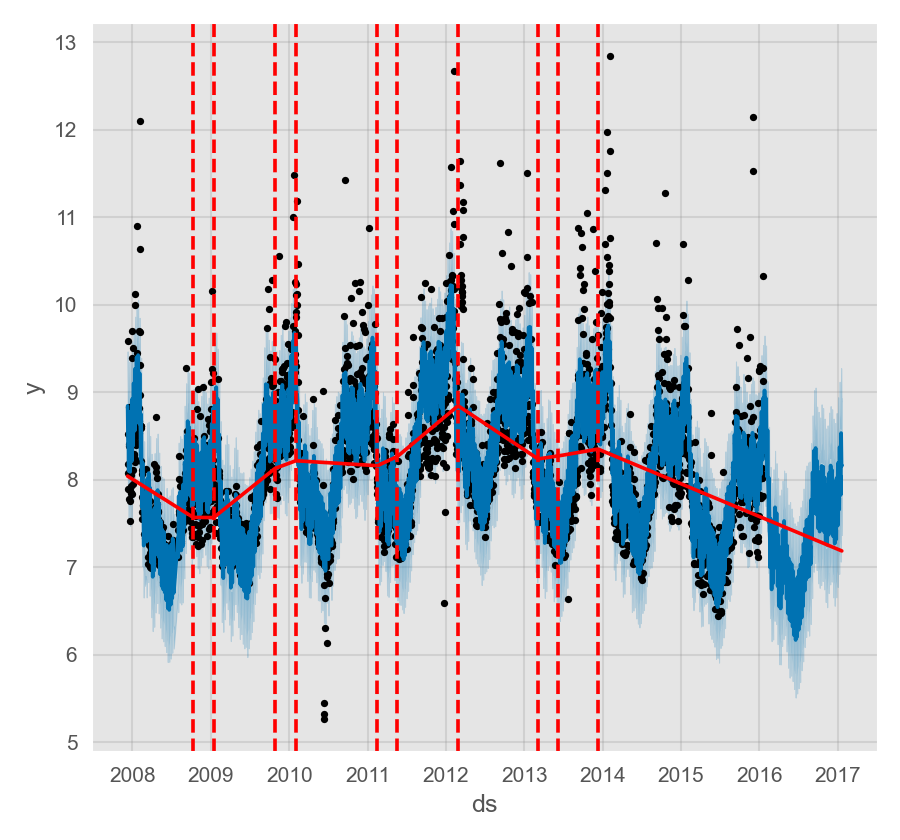
Prophet 趋势突变点
Prophet 趋势突变点
Prophet 趋势突变点
Prophet 季节性和节假日效应
对节假日进行建模时需要创建一个新数据框,其包含两列(节假日 holiday 和日期戳 ds )。数据框必须包含所有出现的节假日,无论是历史数据中还是待预测的数据中。如果这些节假日并没有在待预测的数据中被注明, Prophet 也会利用历史数据对它们建模,但预测未来时却不会使用这些模型来预测。
在这个数据框基础上再新建两列 lower_window 和 upper_window ,从而将节假日的时间扩展成一个区间 [lower_window, upper_window] 。例如将平安夜也加入到 “圣诞节” 里,就设置 lower_window=-1, upper_window=0;如果想将黑色星期五加入到 “感恩节” 里,就设置 lower_window=0, upper_window=1。
下面我们创建一个数据框,其中包含了所有 Peyton Manning 参加过的决赛日期:
playoffs = pd.DataFrame({
'holiday': 'playoff',
'ds': pd.to_datetime([
'2008-01-13', '2009-01-03', '2010-01-16',
'2010-01-24', '2010-02-07', '2011-01-08',
'2013-01-12', '2014-01-12', '2014-01-19',
'2014-02-02', '2015-01-11', '2016-01-17',
'2016-01-24', '2016-02-07']),
'lower_window': 0,
'upper_window': 1})
superbowls = pd.DataFrame({
'holiday': 'superbowl',
'ds': pd.to_datetime([
'2010-02-07', '2014-02-02', '2016-02-07']),
'lower_window': 0,
'upper_window': 1})
holidays = pd.concat((playoffs, superbowls))Prophet 季节性和节假日效应
上述代码中我们将超级碗的日期记录在了决赛的日期数据框中,也记录在了超级碗的日期数据框中。这会造成超级碗日期的效应会在决赛日期的作用下叠加两次。
一旦这个数据框创建好了,就可以通过传入 holidays 参数使其在预测时考虑上节假日效应。这里我们仍以 Peyton Manning 的数据为例:
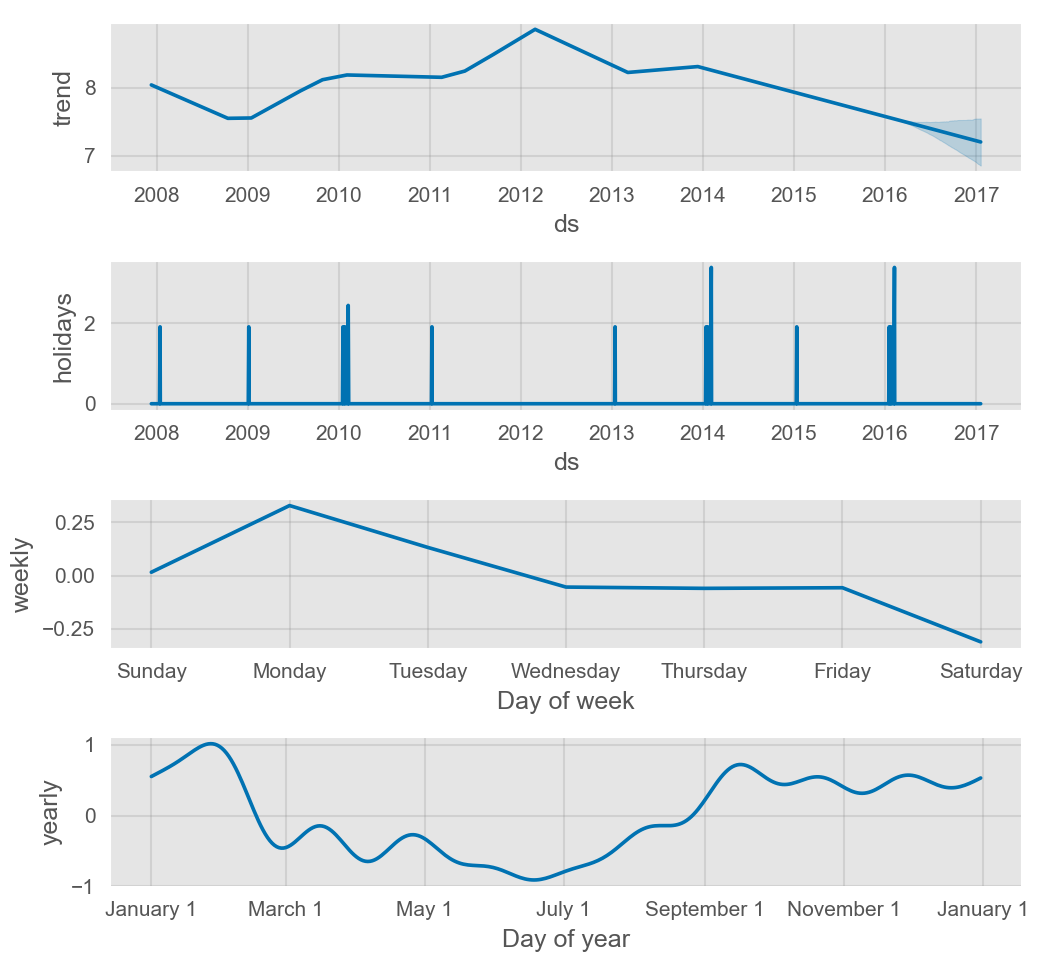
可通过 forecast 数据框,来展示节假日效应:
ds playoff superbowl
2190 2014-02-02 1.219131 1.221194
2191 2014-02-03 1.908490 1.474741
2532 2015-01-11 1.219131 0.000000
2533 2015-01-12 1.908490 0.000000
2901 2016-01-17 1.219131 0.000000
2902 2016-01-18 1.908490 0.000000
2908 2016-01-24 1.219131 0.000000
2909 2016-01-25 1.908490 0.000000
2922 2016-02-07 1.219131 1.221194
2923 2016-02-08 1.908490 1.474741Prophet 季节性和节假日效应
Prophet 季节性和节假日效应
可以利用 add_country_holidays 方法使用内置的特定国家地区的节假日。指定国家地区的名称,则除了利用 holidays 设置的节假日外,这些国家地区的主要节日也会被添加到模型中。
<prophet.forecaster.Prophet at 0x1383bf380>利用 train_holiday_names 可以查看所包含的节假日:
0 playoff
1 superbowl
2 New Year's Day
3 Memorial Day
4 Independence Day
5 Labor Day
6 Veterans Day
7 Thanksgiving Day
8 Christmas Day
9 Christmas Day (observed)
10 Martin Luther King Jr. Day
11 Washington's Birthday
12 Columbus Day
13 Veterans Day (observed)
14 Independence Day (observed)
15 New Year's Day (observed)
dtype: objectProphet 季节性和节假日效应
每个国家中的节假日由 holidays 扩展包提供,可用的国家及其名称详见这里。除此之外,Prophet 还提供了以下国家的节假日:巴西(BR),印度尼西亚(ID),印度(IN),马来西亚(MY),越南(VN),泰国(TH),菲律宾(PH),土耳其( TU),巴基斯坦(PK),孟加拉国(BD),埃及(EG),中国(CN)和俄罗斯(RU)。
在 Python 中,大部分节假日是可以确定性计算的,因此适用于任何日期范围,如果日期超过了一些国家地区的支持的范围则会发出警告。如上所述,国家地区级别的节假日也将展现在组成部分图中:
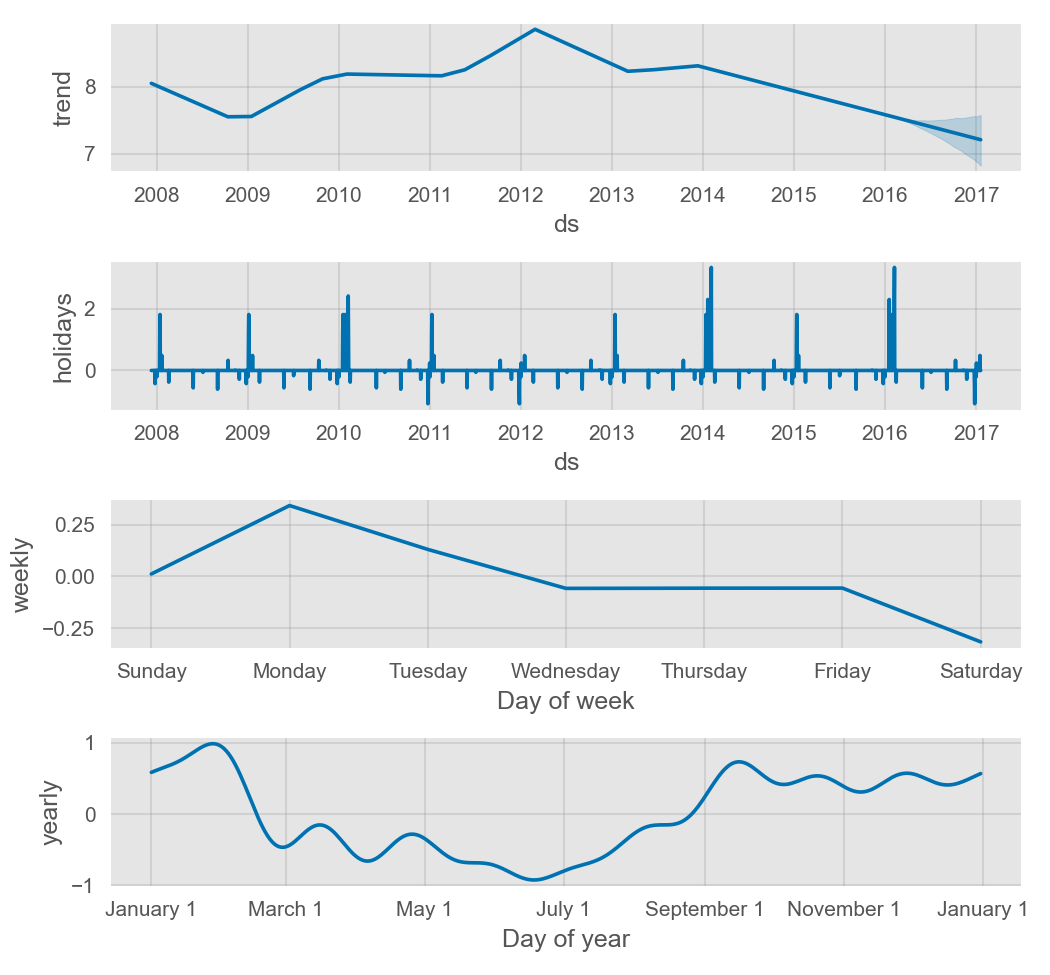
Prophet 季节性和节假日效应
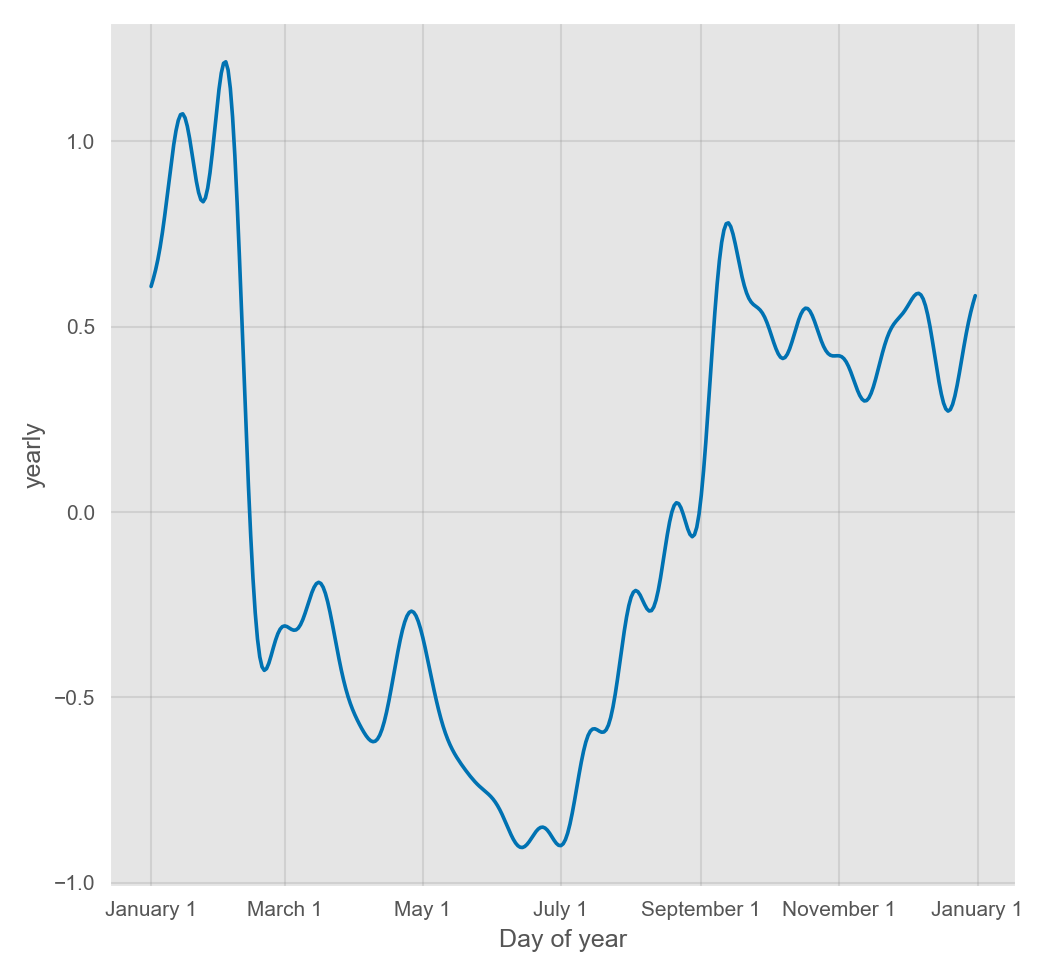
季节性是利用一个 Partial Fourier Sum 进行估计的,具体计算过程详见论文。Wikipedia 中的这张图描述了一个 Partial Fourier Sum 是如何逼近一个任意的周期性信号的。Partial Sum 中项的个数决定了季节性变化的快慢。年度季节性的默认傅立叶阶数为 10:
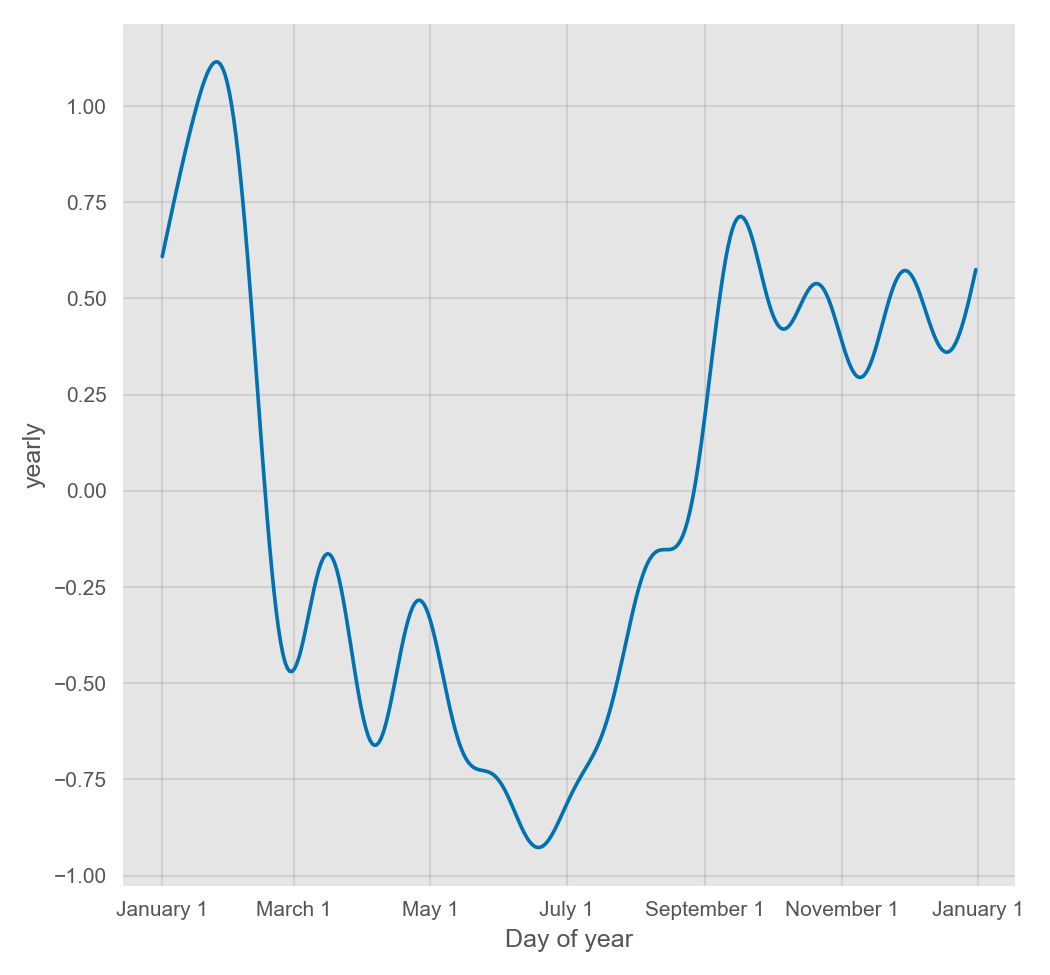
Prophet 季节性和节假日效应
Prophet 季节性和节假日效应
如果时间序列长度在两个周期以上,Prophet 将会默认拟合周和年的季节性,对于日以下尺度时间序列会拟合日季节性。利用 add_seasonality 方法可以添加其他季节性,例如:月,季度,小时尺度的季节性。
该函数的参数分别为:季节性名称,以天为单位的季节性周期,以及季节性傅立叶阶数。默认情况下,Prophet 对于周季节性使用傅立叶阶数为 3,对于年季节性使用傅立叶阶数为 10。

Prophet 季节性和节假日效应
在某些情况下,季节性可能取决于其他因素,例如:周的季节性模式在夏季与一年中其他月份会有所不同;日的季节性模式在工作日和休息日是不同的。这些类型的季节性可以利用条件季节性进行建模。
以 Peyton Manning 数据为示例,默认的周季节性假设周季节性模式在一年中是相同的,但我们希望周季节性模式在赛季(每个周日均有比赛)和非赛季是不同的。我们也可以利用条件季节性来构建赛季和非赛季不同的周季节性。
Prophet 季节性和节假日效应
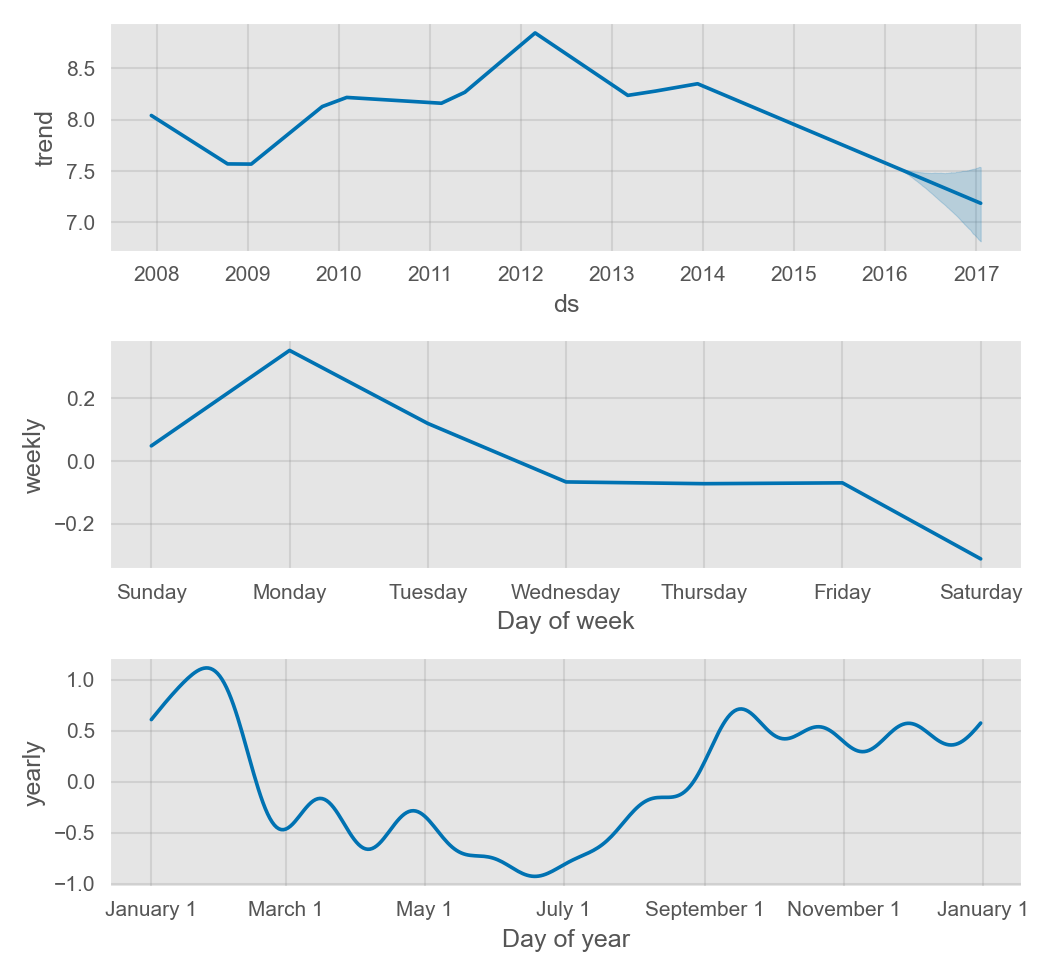
两个季节性均可以从组成部分图中显示。可以看出,在每周日均进行比赛的赛季,周日和周一会有大量的增长,而在非赛季则完全没有。
m = Prophet(weekly_seasonality=False).add_seasonality(
name='weekly_on_season', period=7, fourier_order=3,
condition_name='on_season').add_seasonality(
name='weekly_off_season', period=7,
fourier_order=3, condition_name='off_season')
future['on_season'] = future['ds'].apply(
is_nfl_season)
future['off_season'] = ~future['ds'].apply(
is_nfl_season)
forecast = m.fit(df).predict(future)
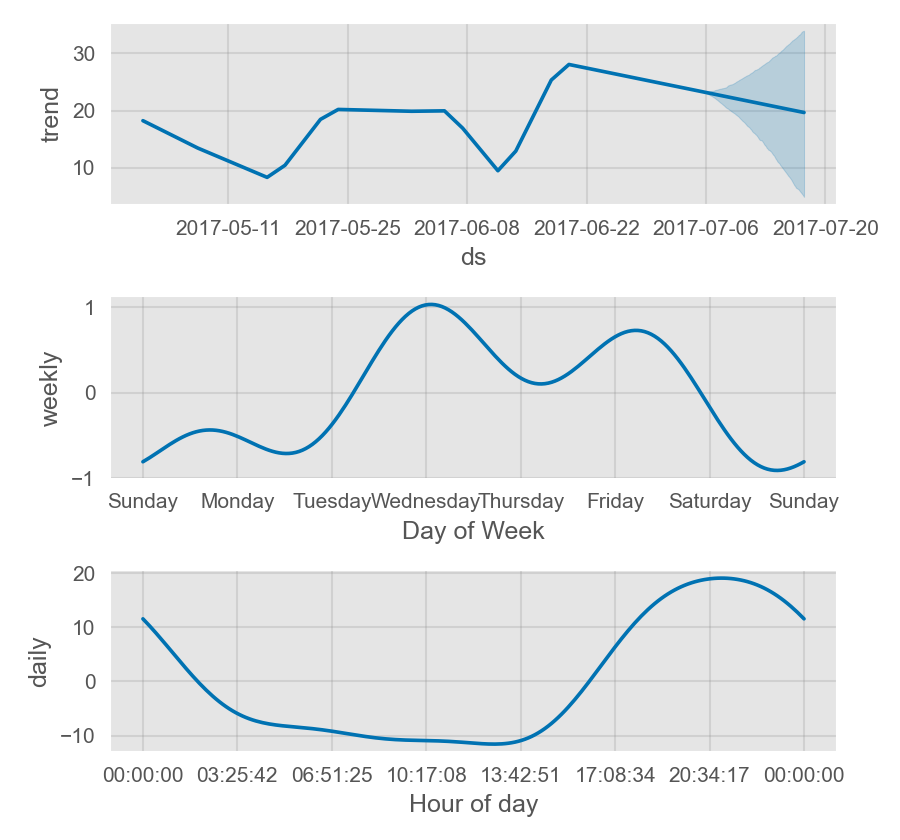
fig = m.plot_components(forecast)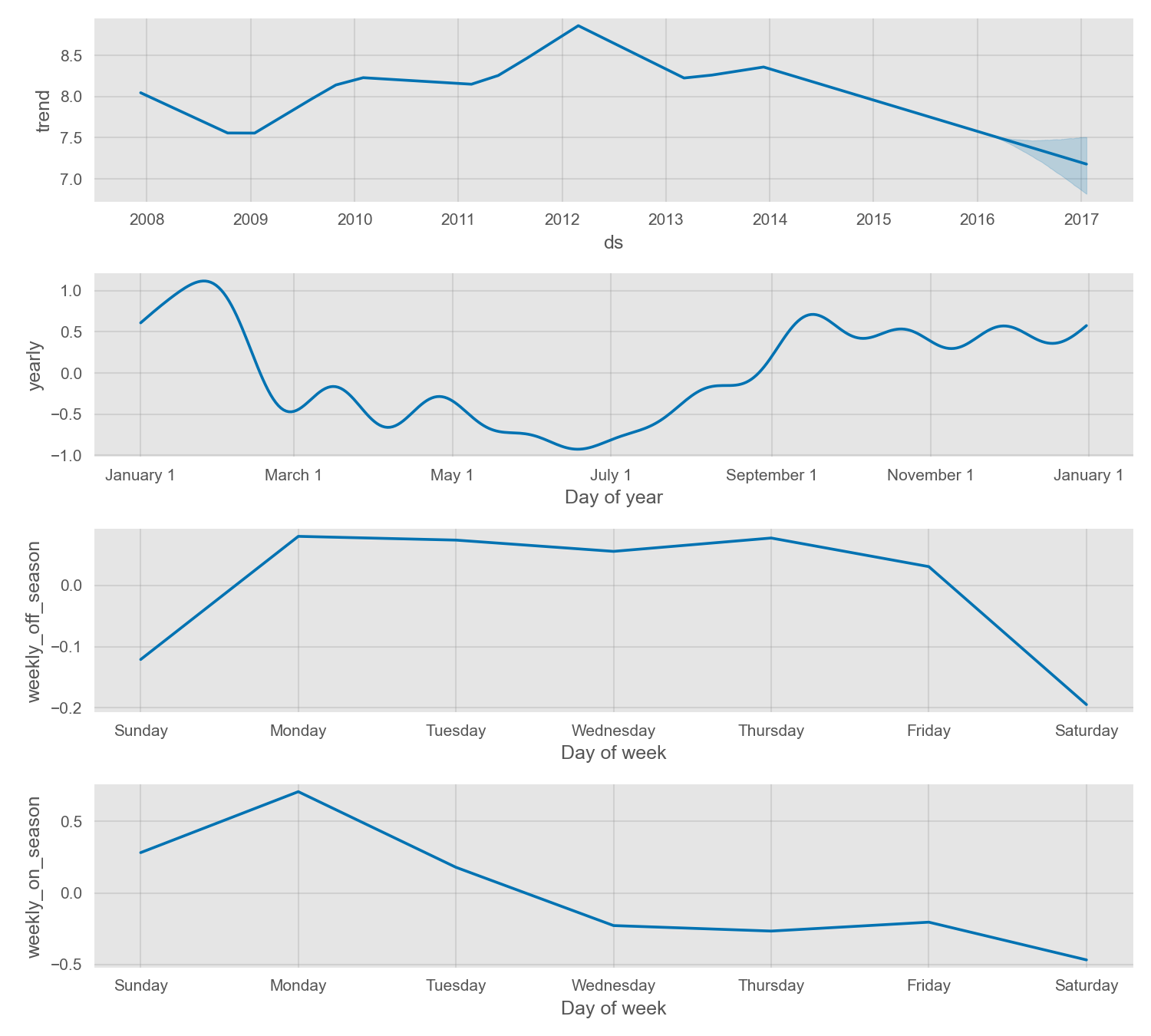
Prophet 季节性和节假日效应
如果发现节假日效应被过度拟合了,通过设置参数 holidays_prior_scale 可以调整它们的先验程度来使之平滑,默认情况下,该参数值为 10,这仅包含了很少的正则化,减少这个参数值可以抑制节假日效应。
<prophet.forecaster.Prophet at 0x138de1a60> ds playoff superbowl
2190 2014-02-02 1.209303 0.965417
2191 2014-02-03 1.856933 0.992110
2532 2015-01-11 1.209303 0.000000
2533 2015-01-12 1.856933 0.000000
2901 2016-01-17 1.209303 0.000000
2902 2016-01-18 1.856933 0.000000
2908 2016-01-24 1.209303 0.000000
2909 2016-01-25 1.856933 0.000000
2922 2016-02-07 1.209303 0.965417
2923 2016-02-08 1.856933 0.992110Prophet 季节性和节假日效应
和之前相比,节假日效应有所降低,尤其是对于观测数据最少的超级碗。还有一个参数 seasonality_prior_scale 可以类似地调整模型对季节性的数据拟合程度。
通过在数据框中增加一列 prior_scale 可以为每个单独的节假日设置不同的先验规模,通过 add_seasonality 可以为每个季节性设置先验程度。例如:设置每周的季节性:
Prophet 季节性和节假日效应
Prophet 乘法型季节性
Prophet 乘法型季节性
Prophet 乘法型季节性
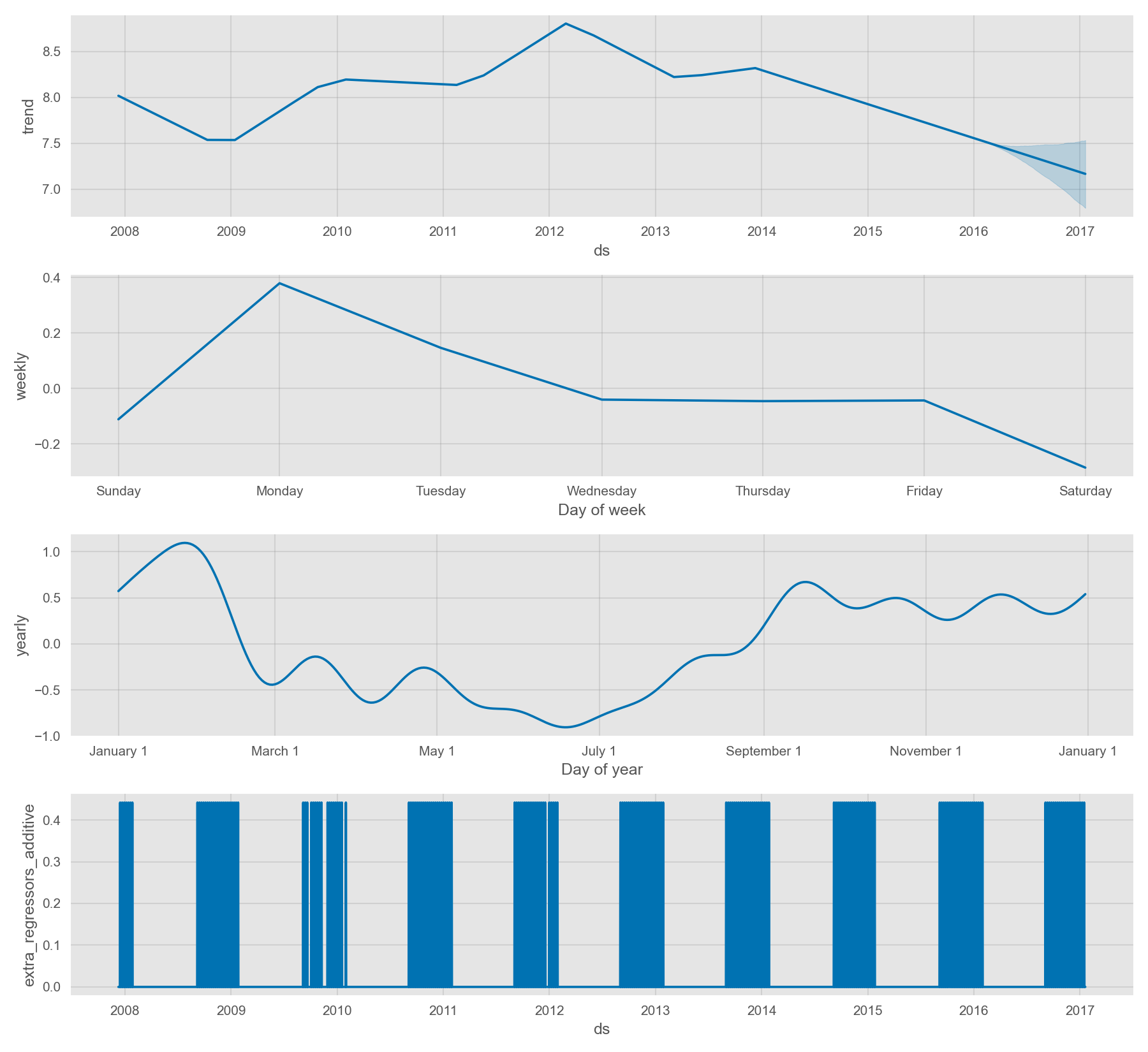
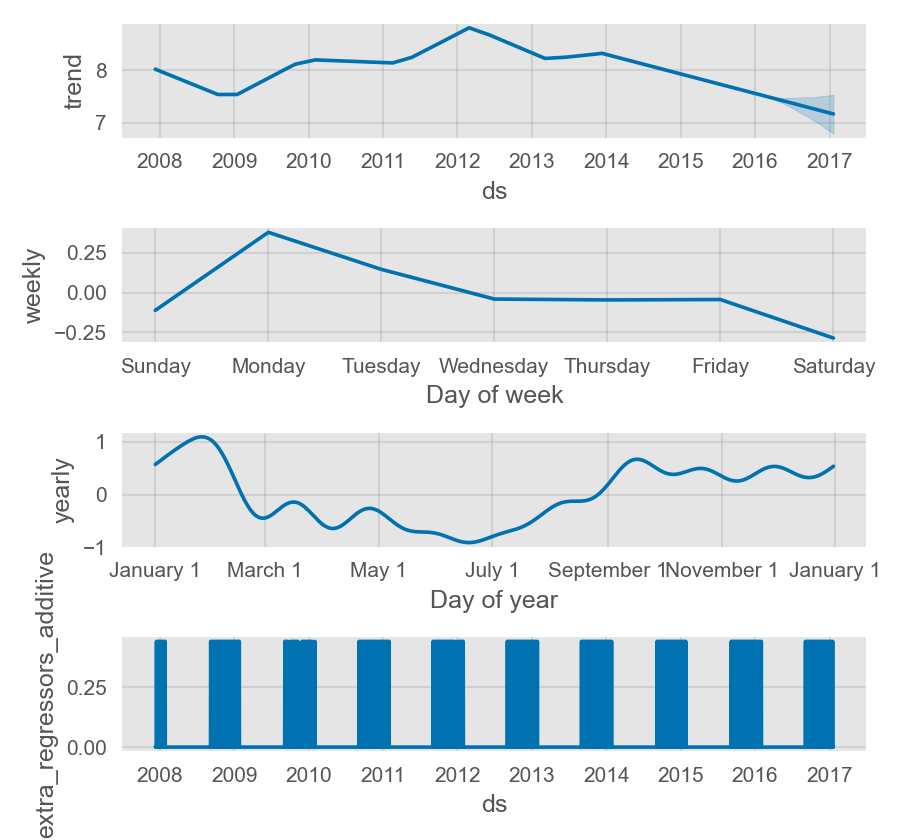
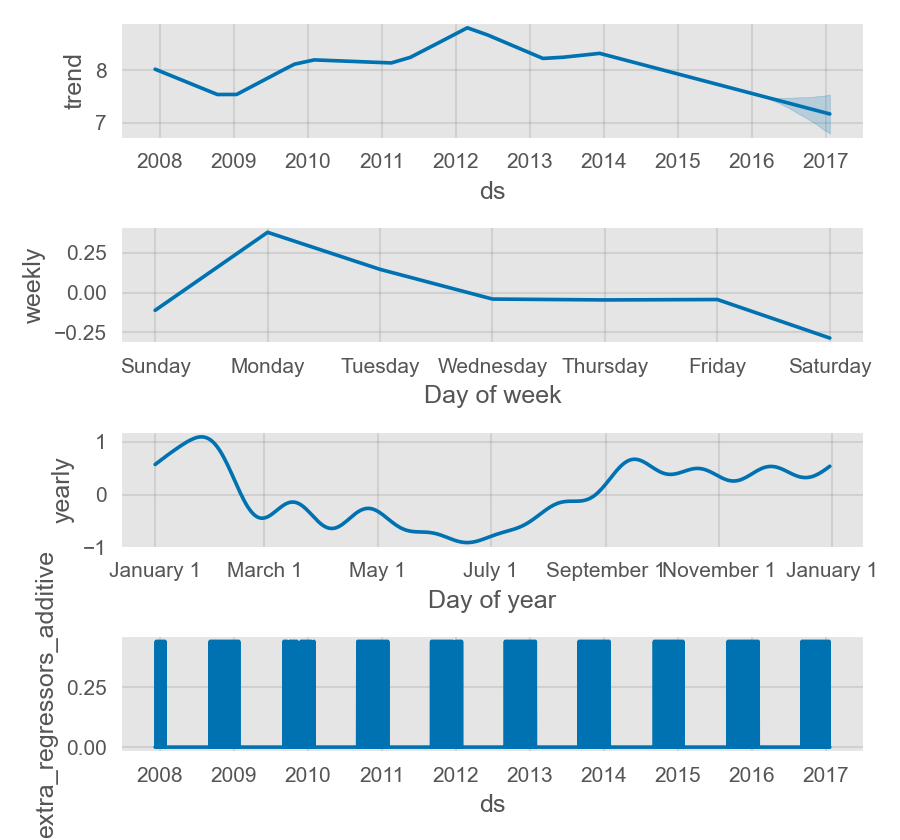
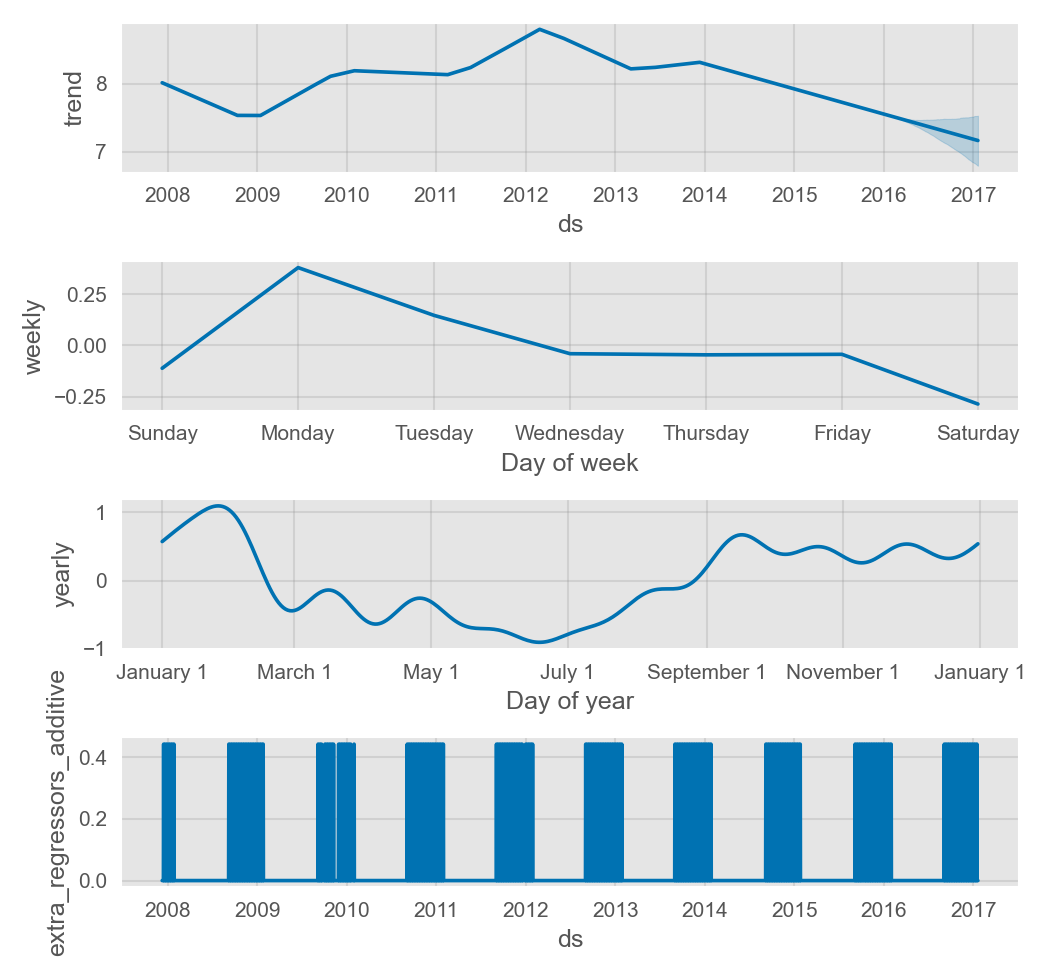
季节性将在组成部分图中展现为趋势的百分比:
通过设置 seasonality_mode='multiplicative',节假日效应也可以建模为乘法模型。任何添加的季节性或回归变量也会使用相同类型的模型,但其也可以单独传入自己所需的类型。例如,下面的示例中设置了一个外部的乘法型季节性模型,但其包括了一个加法型季度季节性因子和一个加法型回归变量:
Prophet 预测区间
默认情况下,Prophet 会对预测值 yhat 返回预测区间,这些预测区间的估计需要建立在一些重要的前提假设之下。在预测时,不确定性来源于三个部分:趋势中的不确定性,季节性估计的不确定性和噪声。
预测中,不确定性最大的来源就在于未来趋势的改变。在之前内容中的时间序列示例中,可以发现历史数据具有明显的趋势性。 Prophet 能够检测到并去拟合它,但是我们期望得到的趋势变化又会如何改变呢?或许这无法确定,因此我们需要尽可能地做出最合理的推断,我们假定 “未来将会和历史具有相似的趋势” 。尤其重要的是,我们假定未来趋势的平均变动频率和幅度和我们观测到的历史值是一样的。通过预测这些趋势变化,并计算它们的分布来确定预测区间。
这种测量不确定性的方法具有以下性质:变化速率灵活性更大时(通过增大参数 changepoint_prior_scale 的值),预测的不确定性也会随之增大。原因在于如果将历史数据中更多的变化速率加入了模型,也就代表我们认为未来也会变化得更多,就会使得预测区间成为反映过拟合的标志。预测区间的宽度(默认值为 80% )可以通过设置 interval_width 参数来控制:
同样,由于预测区间估计时假定未来将会和过去保持一样的变化频率和幅度,而这个假定可能并不正确,所以预测区间的估计不可能完全准确。
Prophet 预测区间
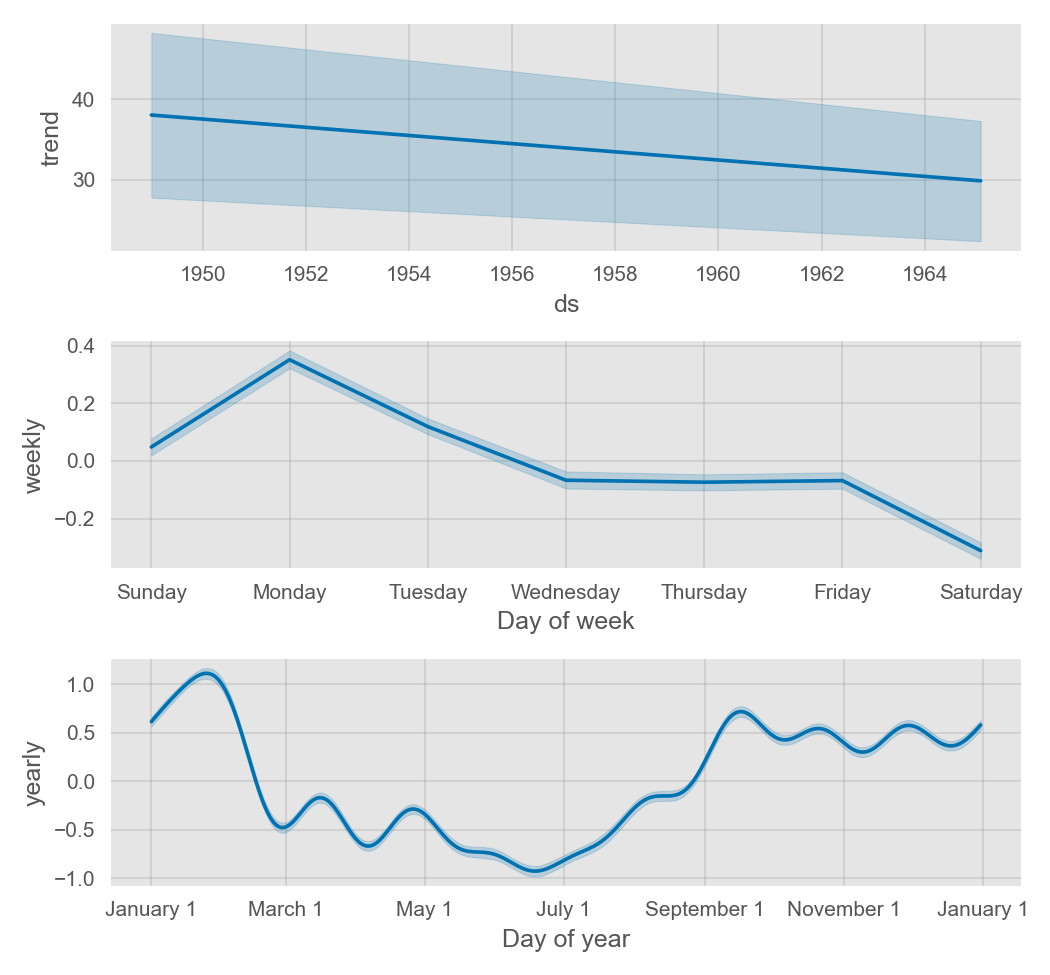
默认情况下, Prophet 只会返回趋势和观测值噪声中的不确定性。为了获取季节效应的不确定性,必须进行完整的贝叶斯采样。这可以通过设置 mcmc_samples 参数(默认值为 0 )来实现。以 Peyton Manning 数据为例:
这将采用 MCMC 采样替代 MAP 估计,并可能需要更长的时间,具体取决于观测的数据量。如果进行了完全采样,就会在组成部分图中看到季节性的不确定性。利用 m.predictive_samples(future) 方法可以获得原始的后验预测样本。
Prophet 异常值
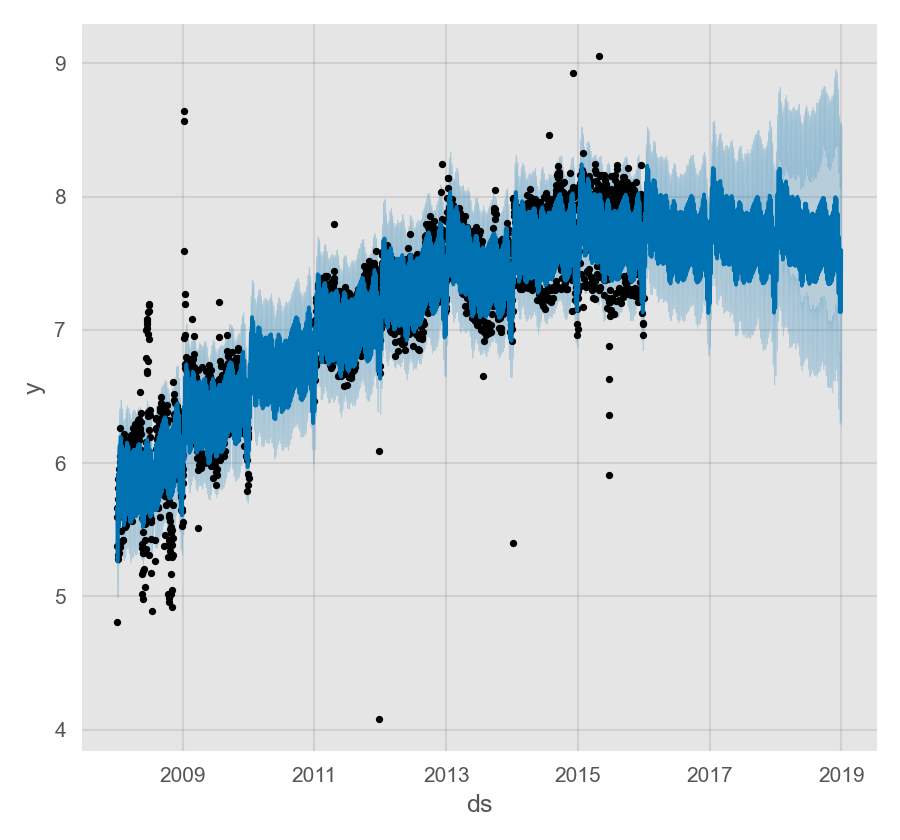
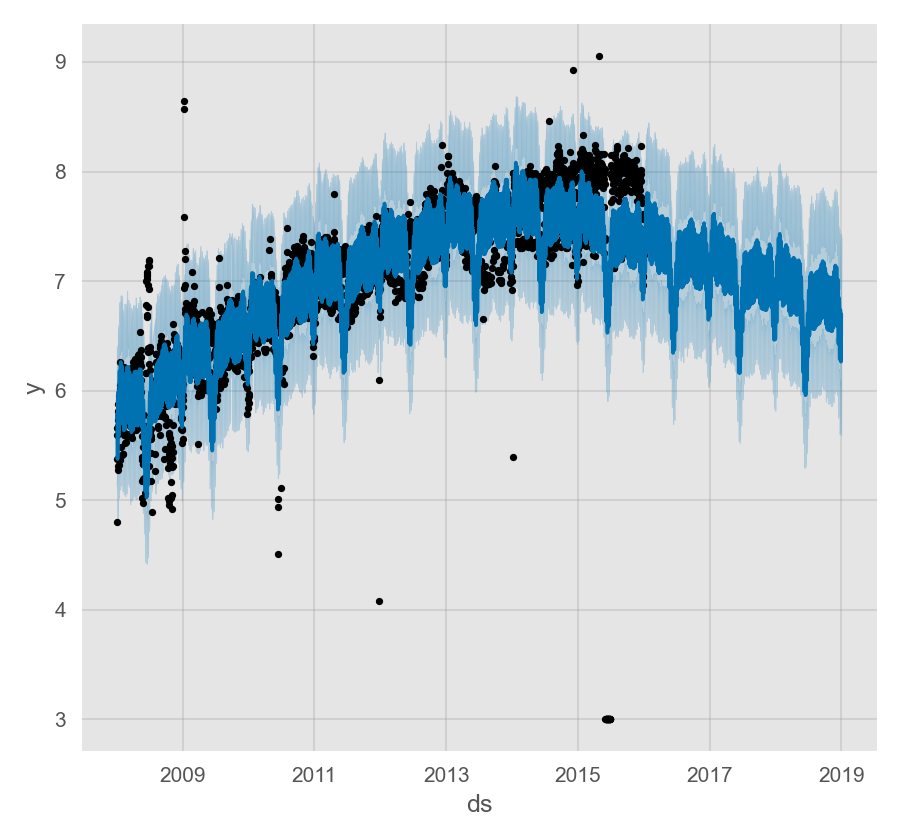
异常值主要通过两种方式影响 Prophet 预测结果。下面我们使用之前使用过的 R 语言维基百科主页对数访问量的数据来建模预测,但其中包含了大量错误数据:
趋势预测似乎是合理的,但预测区间过宽。Prophet 可以处理历史数据中的异常值,但只能通过拟合趋势变化来解决。不确定性模型会以相似的幅度预计未来的趋势变化。

Prophet 异常值
Prophet 异常值
Prophet 异常值
Prophet 非日尺度数据
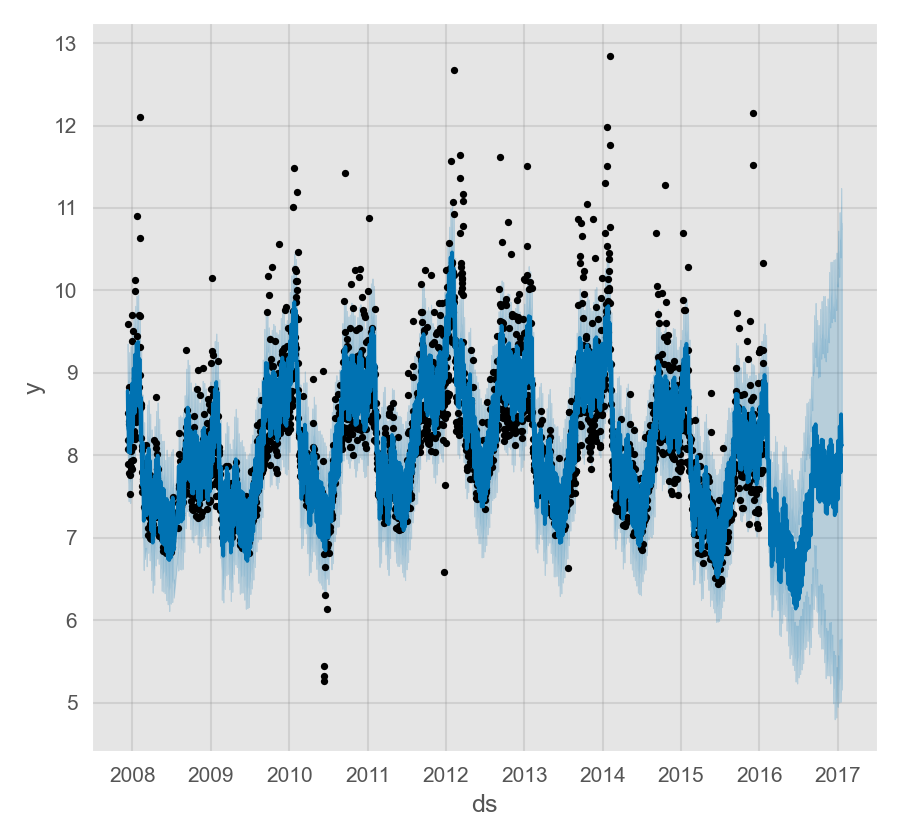
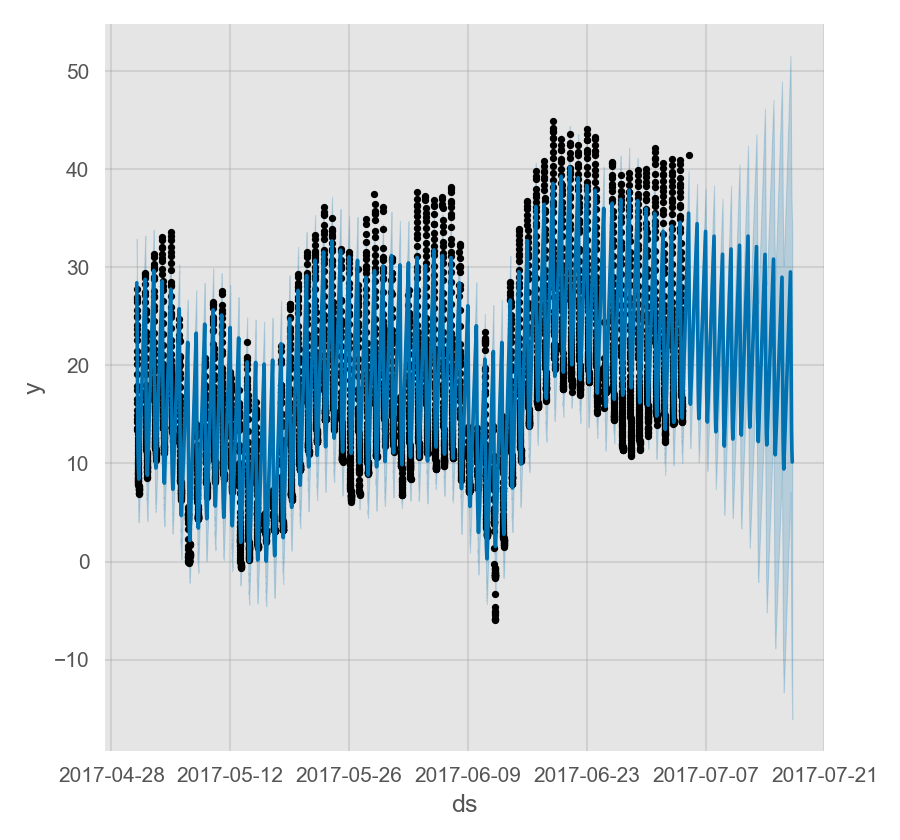
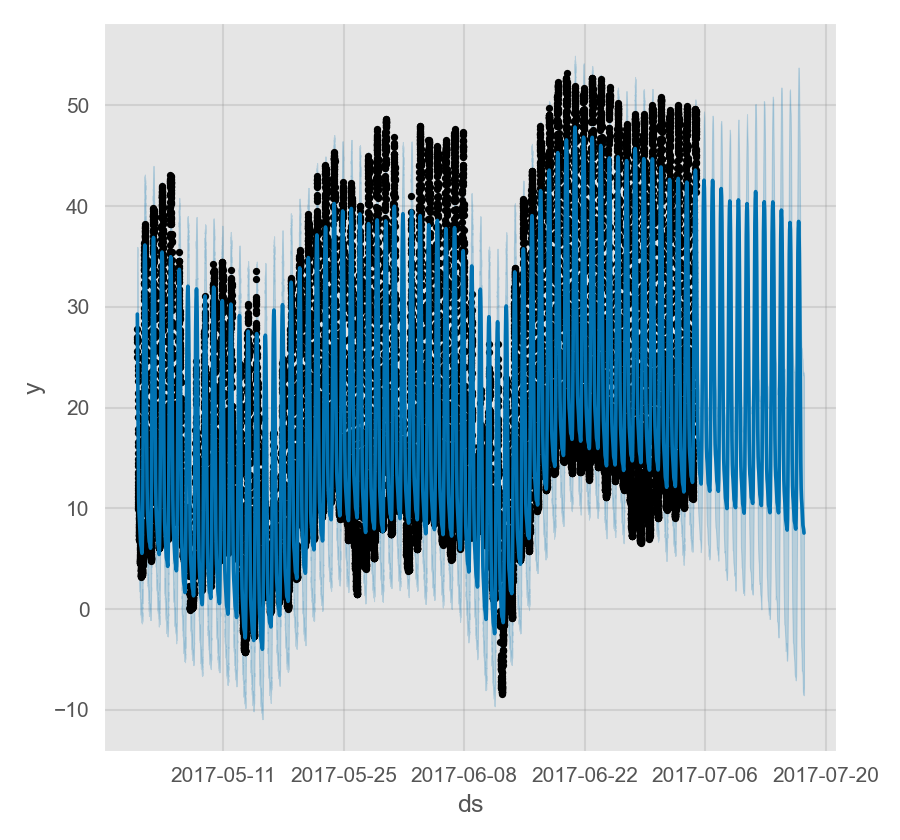
通过在数据框中添加带有时间戳的 ds 列可以让 Prophet 预测非日尺度的时间序列。时间戳的格式应为 YYYY-MM-DD HH:MM:SS。当使用非日尺度的数据时,模型会自动拟合日尺度的季节性。下面示例为一个以 5 分钟为间隔的 Yosemite 地区每日的气温数据:
Prophet 非日尺度数据
Prophet 非日尺度数据
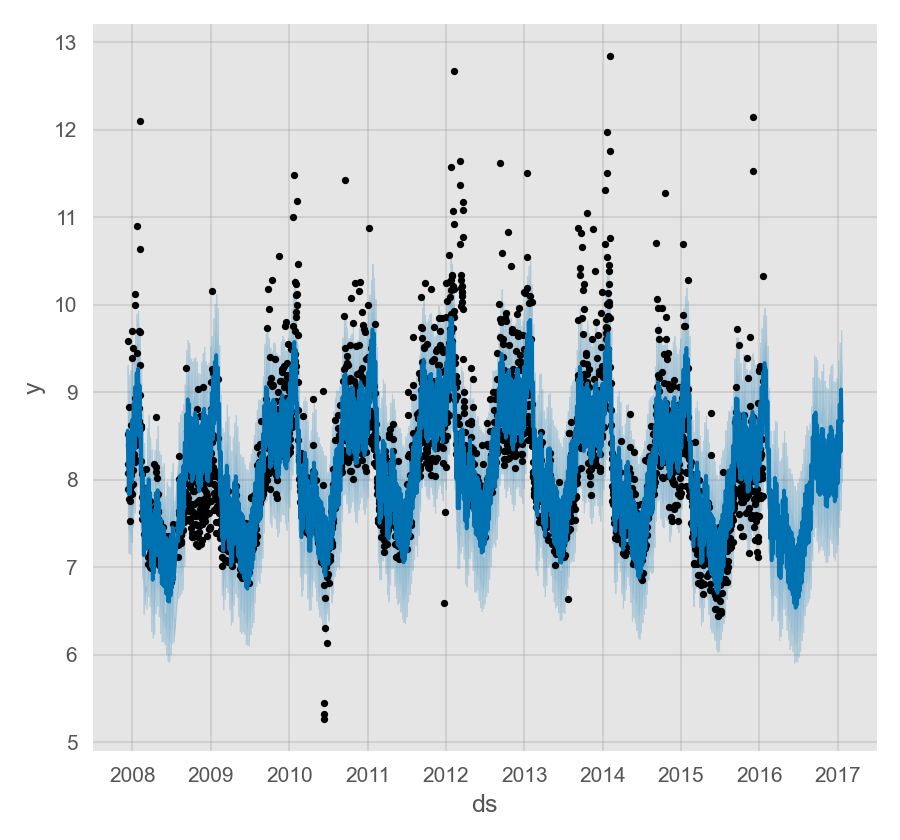
假设上面的数据集只有 0 时至 6 时的观测值:
预测效果似乎很差,未来的波动要比历史数据中大得多。这里的问题是我们仅利用一天中的部分数据(0 时至 6 时)去拟合一整天,因此日尺度的季节性对于一天中剩下的时段是未被很好的估计的。
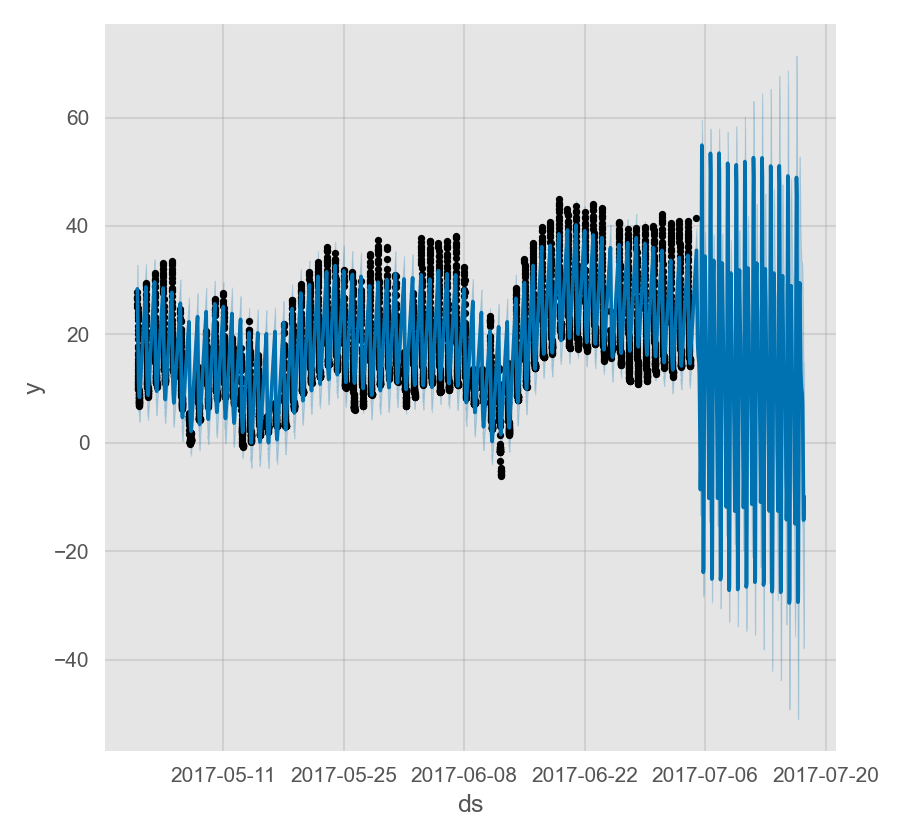
Prophet 非日尺度数据
Prophet 非日尺度数据
Prophet 非日尺度数据
Prophet 非日尺度数据
Prophet 性能评估
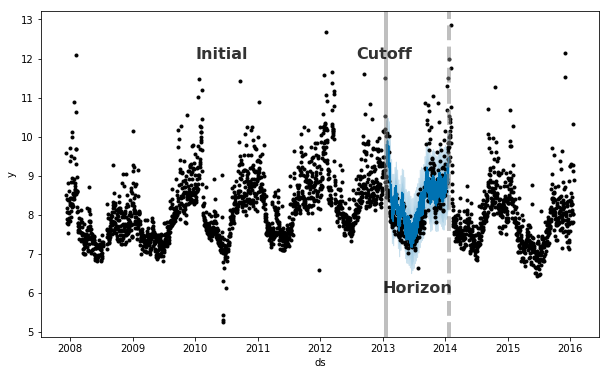
Prophet 提供了时间序列交叉检验的功能,用于利用历史数据来衡量预测误差。这是通过在历史数据中选择截止点来完成的,对于每个截止点仅使用之前的数据来拟合模型。之后可以将预测值和真实值进行比较。右图展示了一个 Peyton Manning 的模拟历史预测,其中模型利用历史数据的开始 5 年进行拟合,并对之后的一年进行了预测。
利用 cross_validation 函数可以对一定范围的历史数据自动地进行交叉检验。通过指定预测时间范围(horizon),然后指定初始训练时间范围的大小(initial)和截止日期之前的时间间隔(period)。
默认情况下,初始训练时间范围为预测时间范围的 3 倍,截止点每半个预测周期一个。
Prophet 性能评估
cross_validation 的输出结果为一个在每个模拟预测日期和截止点日期均包含真实值 y 和预测值 yhat 的数据框。对于 cutoff 和 cutoff + horizon 之间的每个观测点都会进行预测,然后可以利用此数据框计算 y 和 yhat 之间的误差。
下面的交叉检验评估了一个 365 天范围内的预测效果,其利用第一个截止点之前的 730 天数据进行训练,然后每 180 天进行一次预测。在这个 8 年的时间序列中,相当于一共有 11 次预测。
ds yhat yhat_lower yhat_upper y cutoff
0 1994-03-01 181033.202469 163323.893381 202349.282769 192319 1994-02-21
1 1994-04-01 181024.328123 157555.778299 199204.251899 189569 1994-02-21
2 1994-05-01 195058.530271 172696.644398 215441.706349 194927 1994-02-21
3 1994-06-01 188550.706569 166249.857075 206458.012696 197946 1994-02-21
4 1994-07-01 200817.334331 181209.747189 225188.035252 193355 1994-02-21initial, period 和 horizon 应采用 pandas Timedelta 所使用的格式,其接受天数或更短的单位。
Prophet 性能评估
performance_metrics 函数可以计算一些有用的预测性能统计量,包括均方误差(MSE),均方根误差(RMSE),平均绝对误差(MAE),平均绝对百分比误差(MAPE)以及 yhat_lower 和 yhat_upper 的估计范围。这些值通过在 df_cv 上利用滑动窗口计算获得,默认情况下每个滑动窗口中包含 10% 的预测,通过 rolling_window 参数可以改变这个值。
horizon mse rmse mae mape mdape \
0 38 days 1.373044e+08 11717.694045 8603.062879 0.025952 0.020165
1 39 days 1.444286e+08 12017.845742 8819.963077 0.026665 0.020165
2 40 days 1.468964e+08 12120.083801 8961.948426 0.027249 0.022117
smape coverage
0 0.026132 0.557692
1 0.026894 0.557692
2 0.027495 0.538462 Prophet 性能评估
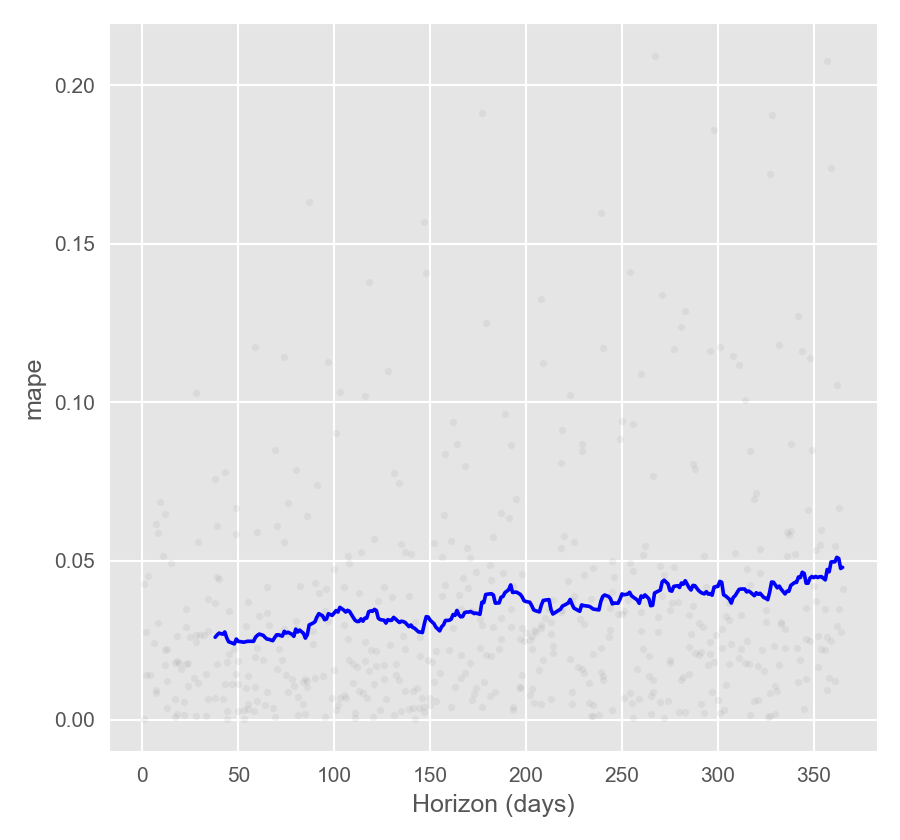
交叉检验的性能指标可以通过 plot_cross_validation_metric 进行可视化。下面的示例中,圆点表示 df_cv 中每个预测的绝对百分比误差,蓝色的线为 MAPE,均值是利用滑动窗口中的圆点的值计算得到。从中可以看出,未来一个月的预测误差在 5% 左右,而一年后的误差会增加到 11% 左右。
增加 rolling_window 的值会让平均曲线更加平滑。初始范围应该足够长以保证捕获模型的所有组成部分,尤其是季节性和额外的回归变量。对于年季节性至少有一年的数据,对于周季节性至少有一周的数据,等等。
感谢倾听
版权所有 © 范叶亮 Leo Van